Econométrie Appliquée

---

---

1 Introduction

Ce document représente une étude économétrique et statistique effectuée dans le contexte de notre cours d’économétrie appliquée dispensé par le Pr. Alain BOUSQUET. Son objectif est de condenser et d’expliquer les résultats les plus significatifs obtenus au cours de notre analyse. Notons que de nombreux résultats qui n’étaient pas explicitement demandés dans les questions ont été inclus, car nous avons estimé qu’ils contribuaient à enrichir nos explications et à fournir un contexte plus complet.

2 Imports et configuration

Note

Tout au long de ce projet, nous utiliserons l’approche tidy développée par Wickham (2014) plutôt que l’approche base R pour manipuler nos données. De plus, l’utilisation du package micEcon et de ses annexes nous facilitera grandement le travail d’estimation – voir Henningsen (2017).

library(ggplot2)
library(dplyr)
library(tidyr)
library(gt)
library(tibble)
library(patchwork)
library(FactoMineR)
library(factoextra)
library(ggtext)
library(micEcon)
library(micEconSNQP)
library(micEconIndex)
library(micEconCES)
library(frontier)
library(ranger)
library(tuneRanger)
library(mlr)
library(rsample)
library(forcats)
library(performance)

3 Description des données

Le jeu de données appleProdFr86 utilisé dans le papier d’économétrie de Ivaldi et al. (1996) comprend des données transversales de production de 140 producteurs de pommes français datant de l’année 1986.

apples <- readxl::read_excel("applied_econ/data/appleProdFr86.xlsx")

Descriptif des colonnes

Colonnes	Description
vCap	Coûts associés au capital (foncier compris).
vLab	Coûts associés au travail (y compris la rémunération du travail familial non rémunéré).
vMat	Coûts des matières intermédiaires (plantations, engrais, pesticides, carburant, etc).
qApples	Indice de quantité des pommes produites.
qOtherOut	Indice de quantité de tous les autres outputs.
qOut	Indice de quantité de toute la production $\Rightarrow 580000\cdot (\text{qApples}+\text{qOtherOut})$
pCap	Indice des prix du capital.
pLab	Indice des prix du travail.
pMat	Indice des prix des matières intermédiaires.
pOut	Indice des prix de la production globale.
adv	Distingue les producteurs qui sont conseillés par des laboratoires d’agronomie.

3.1 Tableau descriptif

Ce tableau descriptif retrace les 10 premières observations et l’ensemble des variables associées dans le dataset.

Producteurs de pommes 🍎
140 producteurs 🇫🇷 (1986)
$N$	Costs			Quantity Index			Price Index				$adv$	Factor Quantities
	$v_{Cap}$	$v_{Lab}$	$v_{Mat}$	$q_{Apples}$	$q_{OtherOut}$	$q_{Out}$	$p_{Cap}$	$p_{Lab}$	$p_{Mat}$	$p_{Out}$		$q_{Cap}$	$q_{Lab}$	$q_{Mat}$
1	220K	320K	300K	1.4	0.98	1.4M	2.6	0.90	8.9	0.66		84K	360K	34K
2	130K	190K	260K	0.86	1.1	1.1M	3.3	0.75	6.4	0.72		40K	250K	41K
3	81K	130K	91K	3.3	0.40	2.2M	2.2	0.96	3.7	0.94		37K	140K	24K
4	34K	110K	60K	0.44	0.44	510K	1.6	1.3	3.2	0.60		21K	83K	19K
5	39K	84K	100K	1.8	0.015	1.1M	0.87	0.94	7.2	0.83		45K	89K	14K
6	120K	520K	580K	8.5	0.43	5.2M	1.0	0.96	9.6	1.4		120K	550K	60K
7	89K	170K	340K	4.1	3.3	4.3M	0.98	1.0	7.8	1.3		91K	170K	44K
8	92K	200K	130K	2.2	1.1	1.9M	1.0	0.92	5.0	0.62		89K	220K	25K
9	66K	180K	190K	1.8	2.6	2.5M	2.5	1.0	5.6	1.9		27K	180K	34K
10	94K	140K	82K	1.6	0.45	1.2M	0.98	0.64	5.6	0.49		95K	220K	15K
Source: Ivaldi et al. (1996)

4 Statistiques descriptives

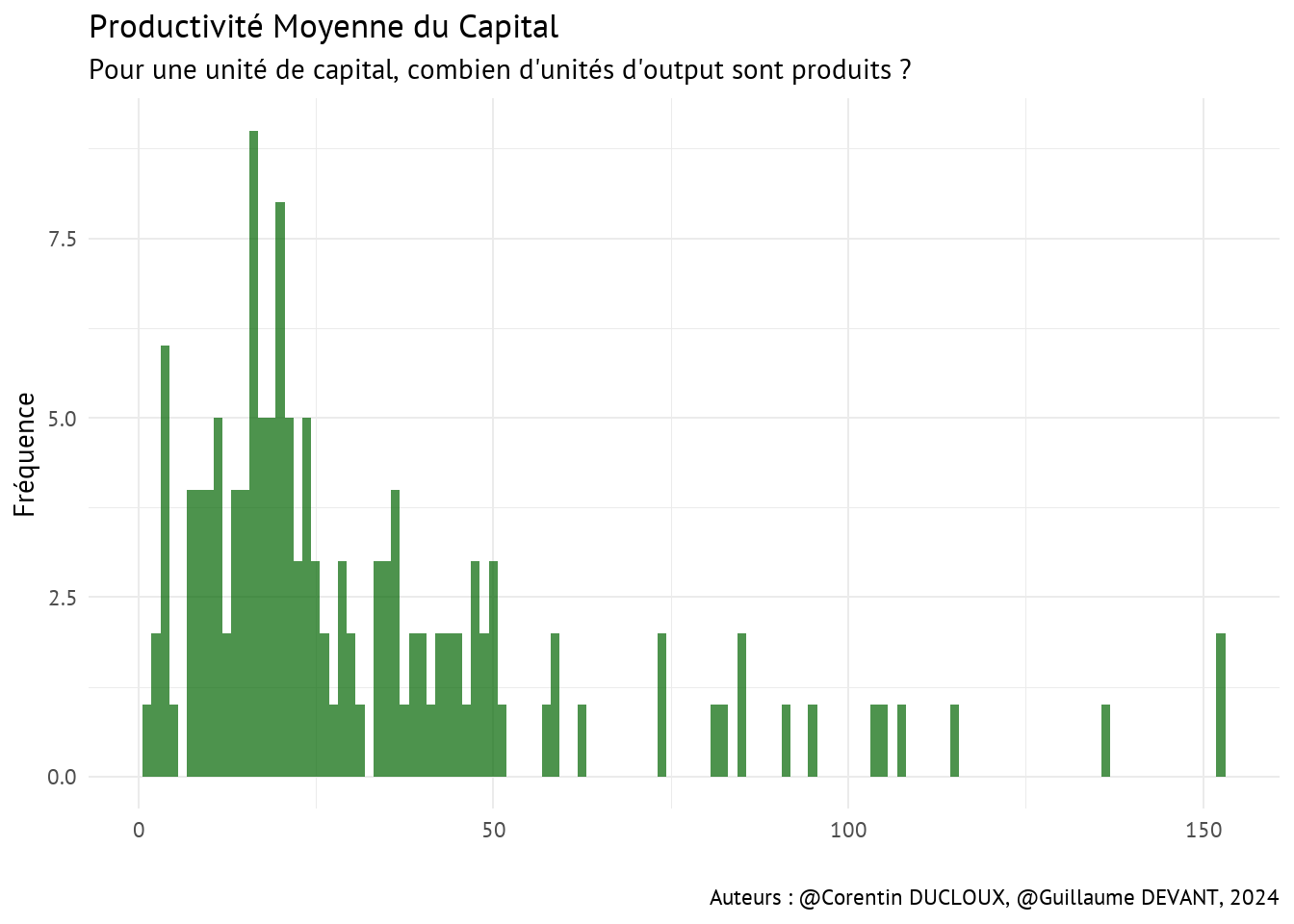
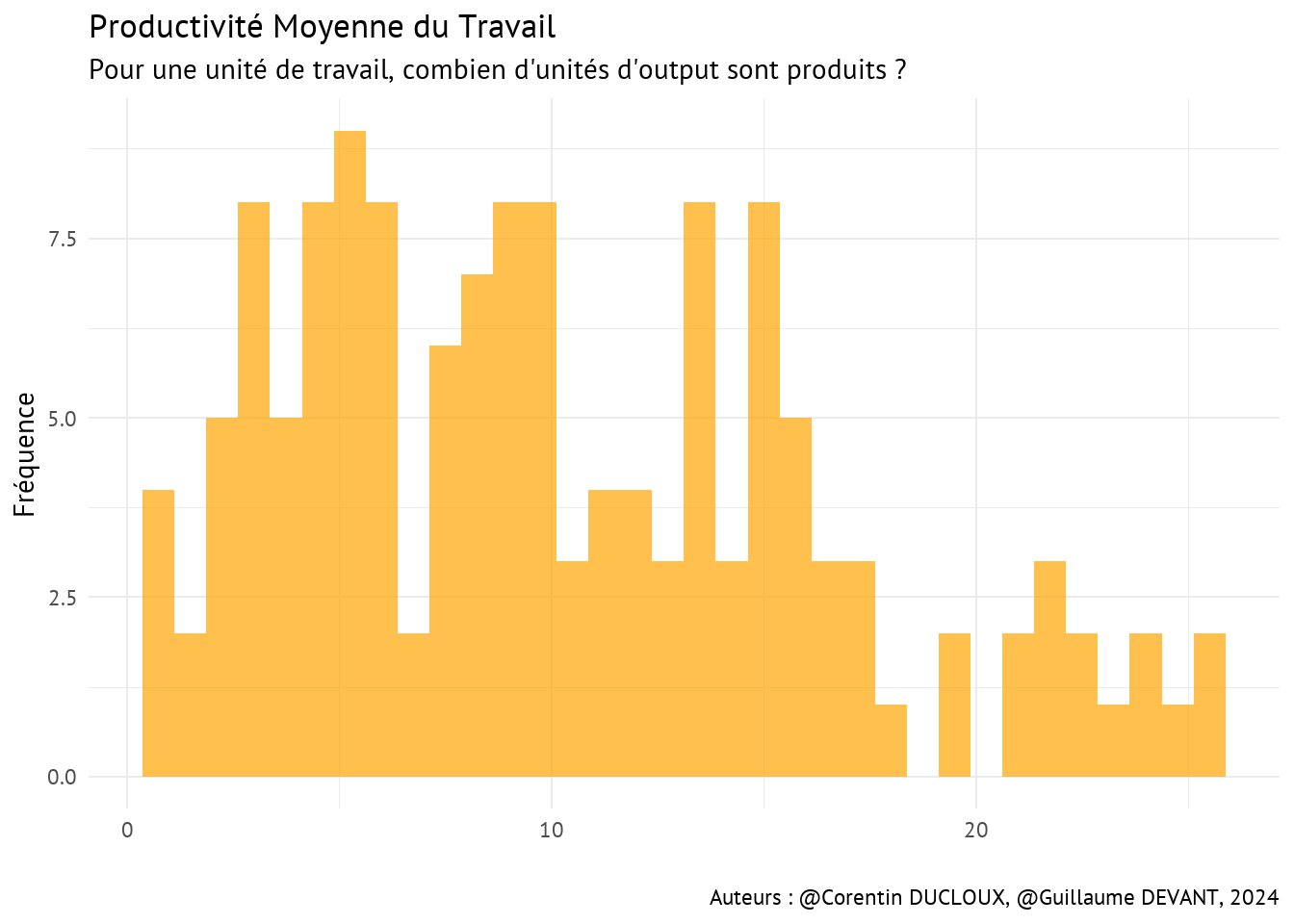
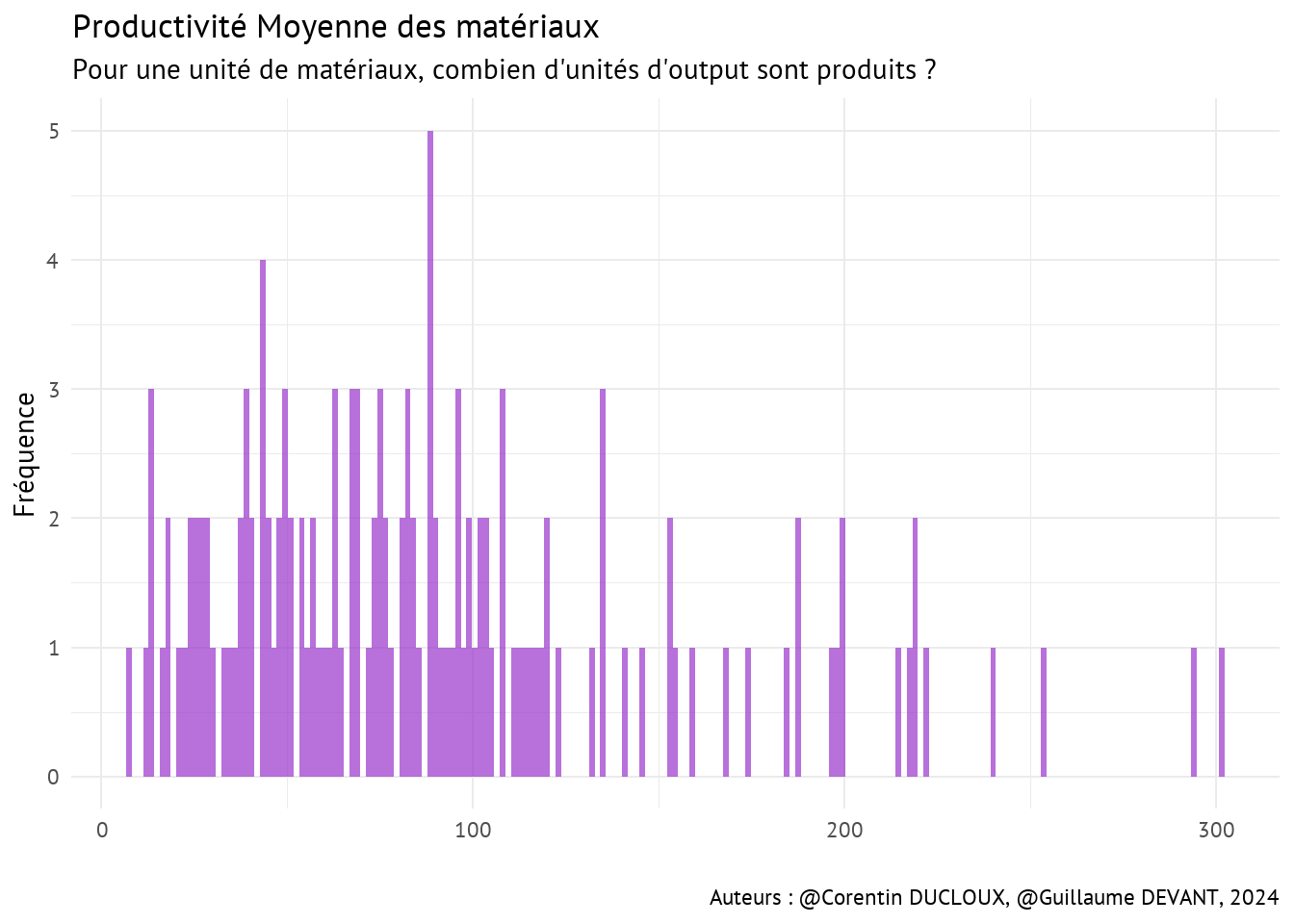
4.1 Productivité moyenne des facteurs de production

La productivité moyenne ($AP=$ Average Product) consiste à diviser la quantité totale d’output par la quantité totale de facteur utilisé (input) dans le processus de production.

Imaginons que les unités d’output sont des tonnes. Pour chaque input, cela revient en fait à expliquer combien de tonnes sont produites en moyenne par unité de capital, de travail et de matières intermédiaires en 1986 pour chaque producteur de pommes.

Nous obtenons alors respectivement :

• $A{P}_{Cap}=\frac{q_{Out}}{q_{Cap}}$

• $A{P}_{Lab}=\frac{q_{Out}}{q_{Lab}}$

• $A{P}_{Mat}=\frac{q_{Out}}{q_{Mat}}$

apples <- apples |> mutate(
    AP_Cap = qOut / qCap,
    AP_Lab = qOut / qLab,
    AP_Mat = qOut / qMat
)

Productivité Moyenne par Facteur 📋
Capital — Travail — Matériaux
	$min$	$\mu$	$max$	${\sigma }^2$
$A{P}_{Cap}$	1.45	32.64	152.87	29.25
$A{P}_{Lab}$	0.86	10.21	25.63	6.20
$A{P}_{Mat}$	8.22	90.64	301.43	60.43

Ce tableau, en plus des visualisations qui vont suivre, permet d’établir que les productivités moyennes par facteur sont très différentes selon les producteurs. De plus, on s’aperçoit aussi qu’investir dans un facteur particulier peut être plus intéressant qu’un autre.

C’est particulièrement vrai pour le facteur qMat avec une productivité moyenne minimale de 8.22 unités d’output pour une unité de matériaux et jusqu’à 301.43 unités d’output pour une unité de matériaux.

Avertissement

Attention néanmoins, la productivité moyenne par facteur ne prend pas en compte le coût associé à chaque facteur de production, il est donc tout à fait possible que le facteur qMat ait une productivité moyenne élevée car son coût moyen est lui aussi elevé.

4.2 Corrélations entre les quantités des 3 facteurs de production

Matrice de corrélation
	$q_{Cap}$	$q_{Lab}$	$q_{Mat}$
$q_{Cap}$	1.00	0.59	0.66
$q_{Lab}$	0.59	1.00	0.79
$q_{Mat}$	0.66	0.79	1.00

• Les quantités des 3 facteurs de production sont toutes corrélées positivement.

• On s’aperçoit que la corrélation positive la plus importante est entre $q_{Lab}$ et $q_{Mat}$ $\Rightarrow$ cela implique que lorsque la quantité de travail augmente, la quantité de matériaux a tendance à augmenter dans un niveau très similaire, et vice versa.

4.3 Corrélations entre les productivités moyennes

Essayons maintenant de comprendre comment les productivités moyennes individuelles sont corrélées :

Matrice de corrélation
	$A{P}_{Cap}$	$A{P}_{Lab}$	$A{P}_{Mat}$
$A{P}_{Cap}$	1.00	0.51	0.46
$A{P}_{Lab}$	0.51	1.00	0.73
$A{P}_{Mat}$	0.46	0.73	1.00

• Ces résultats nous suggèrent l’existence de relations positives entre les productivités moyennes des différents facteurs de production dans le processus de production.

• Ici, une augmentation de la productivité moyenne du travail peut être associée à une augmentation significative de la productivité moyenne des matériaux, ce qui peut être dû à des facteurs tels que des processus de production plus efficaces ou une meilleure utilisation des ressources de la part du producteur de pommes.

---

Note

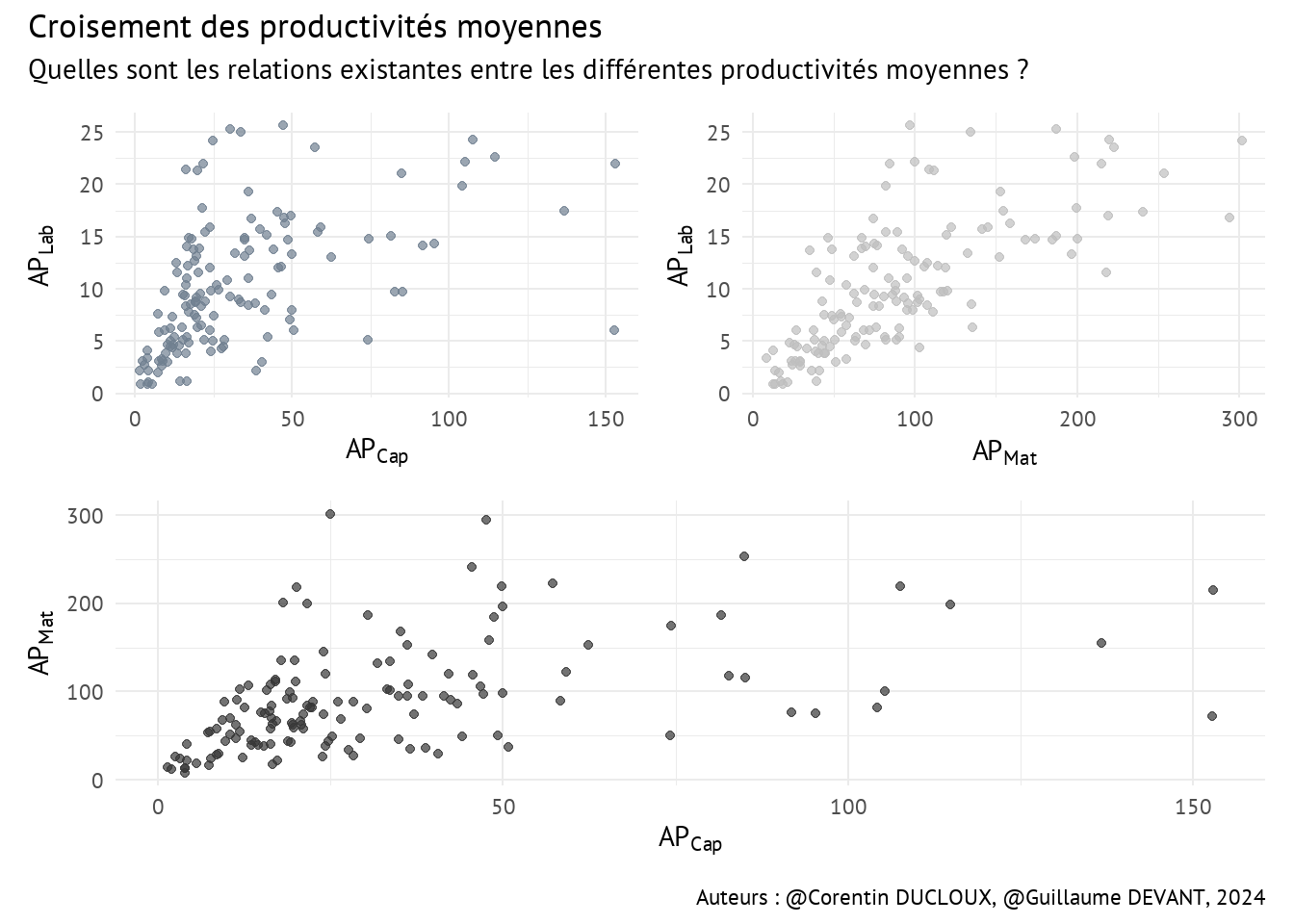
Les représentations des productivités moyennes $A{P}_{Cap}$, $A{P}_{Lab}$ et $A{P}_{Mat}$ par rapport à l’output $q_{Out}$ peuvent aussi être très utiles pour comprendre les relations entre la production totale et l’utilisation des différents facteurs de production.

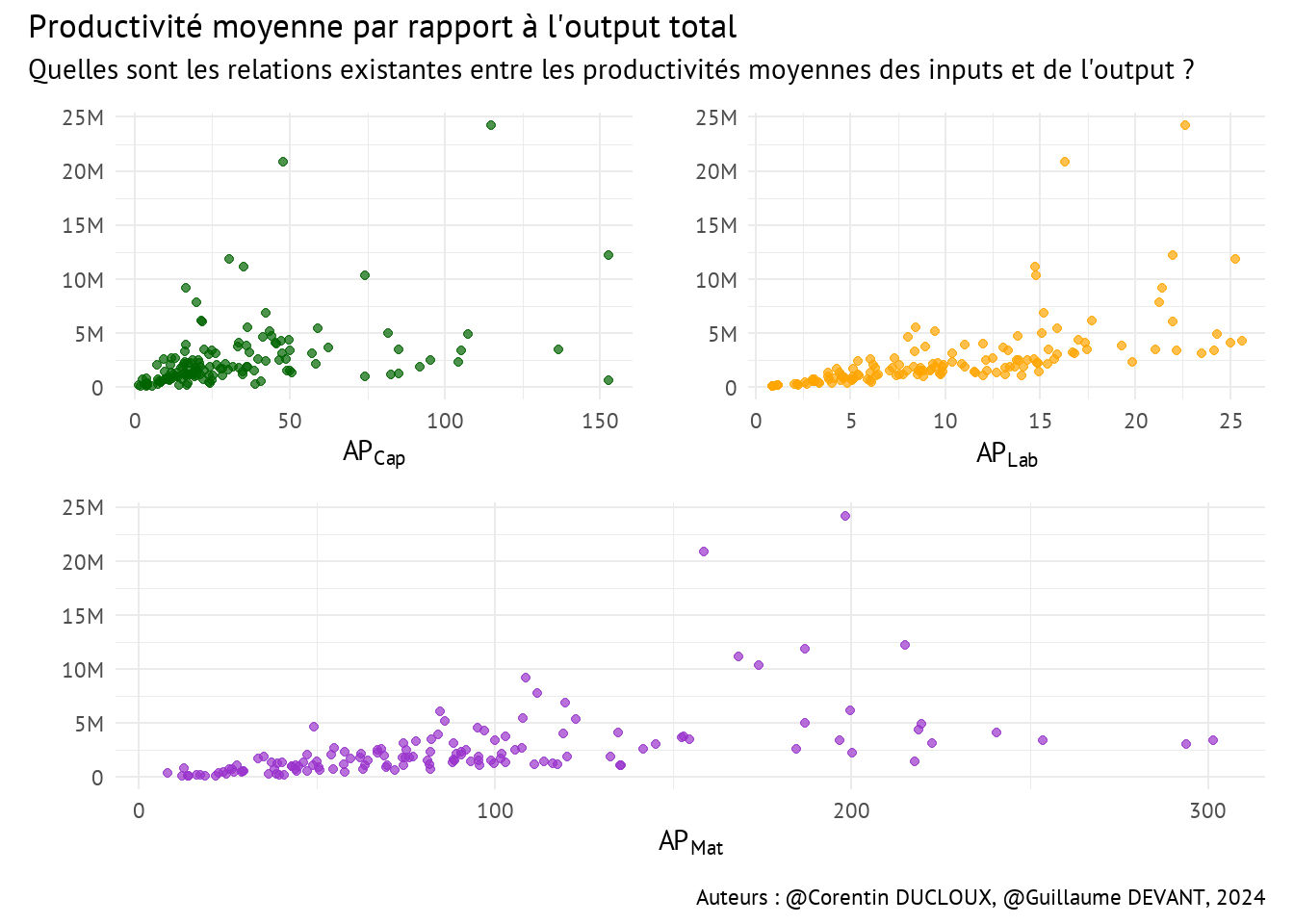
• Les valeurs extrêmes dans ces nuages de points nous permettent de distinguer aisément les producteurs efficaces et inefficaces dans l’utilisation des ressources.

4.4 Indices de Paasche, Laspeyres et Fisher

Les productivités moyennes nous donnent une indication facteur par facteur, mais elles ne nous donnent pas nécessairement d’information globale. Dans ce cadre, on peut alors se demander comment agréger des quantités avec une règle ad hoc en un indice synthétique.

3 Indices principaux existent

Indice de Paasche

$${\text{Paasche}}_{index}=\frac{(v_{Cap}+v_{Lab}+v_{Mat})}{{\overline{q}}_{Cap}\cdot p_{Cap}+{\overline{q}}_{Lab}\cdot p_{Lab}+{\overline{q}}_{Mat}\cdot p_{Mat}}$$

Indice de Laspeyres

$${\text{Laspeyres}}_{index}=\frac{(q_{Cap}\cdot {\overline{p}}_{Cap}+q_{Lab}\cdot {\overline{p}}_{Lab}+q_{Mat}\cdot {\overline{p}}_{Mat})}{({\overline{q}}_{Cap}\cdot {\overline{p}}_{Cap}+{\overline{q}}_{Lab}\cdot {\overline{p}}_{Lab}+{\overline{q}}_{Mat}\cdot {\overline{p}}_{Mat})}$$

Indice de Fisher

$${\text{Fisher}}_{index}=\sqrt{{\text{Paasche}}_{index}\cdot {\text{Laspeyres}}_{index}}$$

De plus, la fonction quantityIndex du package micEconIndex a l’intérêt de facilement intégrer les calculs de chaque indice (Voir ci-dessous).

apples <- apples |> mutate(
    L_Index = quantityIndex(
        prices = c("pCap", "pLab", "pMat"),
        quantities = c("qCap", "qLab", "qMat"),
        data = apples,
        method = "Laspeyres"
    ),
    P_Index = quantityIndex(
        prices = c("pCap", "pLab", "pMat"),
        quantities = c("qCap", "qLab", "qMat"),
        data = apples,
        method = "Paasche"
    ),
    F_Index = quantityIndex(
        prices = c("pCap", "pLab", "pMat"),
        quantities = c("qCap", "qLab", "qMat"),
        data = apples,
        method = "Fisher"
    )
)

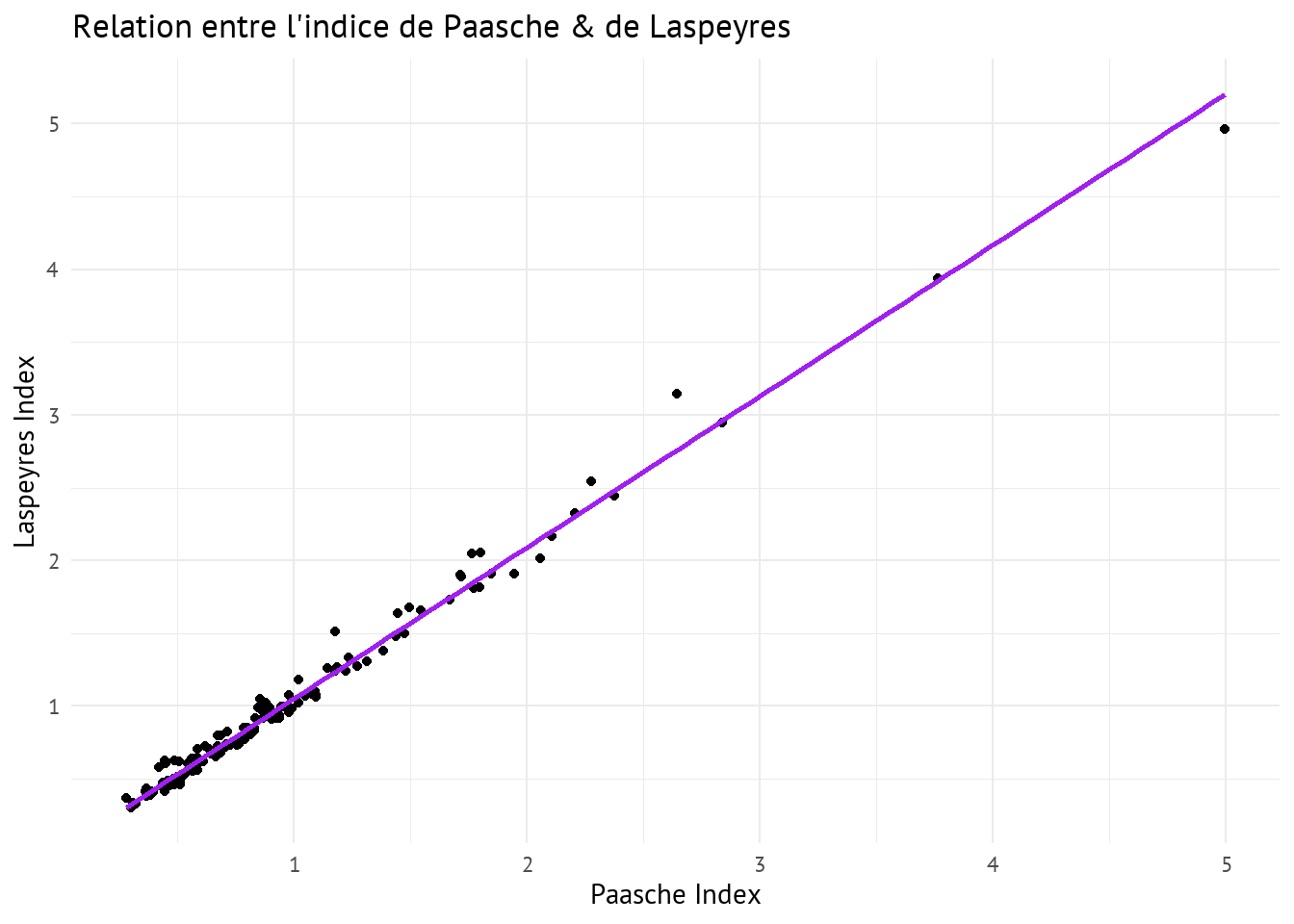
D’après cette visualisation on peut conclure que faire le choix de l’indice de Paasche ou de Laspeyres revient sensiblement à la même interprétation.

Note : Etant donné que l’indice de Fisher est une moyenne géométrique des deux indices, il n’est pas non plus nécessaire de le représenter puisque la relation linéaire entre les deux indices sera presque parfaite dans ce cas.

---

Matrice de corrélation
	$A{P}_{Cap}$	$A{P}_{Lab}$	$A{P}_{Mat}$	${\text{Fisher}}_{index}$
$A{P}_{Cap}$	1.00	0.51	0.46	0.11
$A{P}_{Lab}$	0.51	1.00	0.73	0.36
$A{P}_{Mat}$	0.46	0.73	1.00	0.23
${\text{Fisher}}_{index}$	0.11	0.36	0.23	1.00

• Ces résultats suggèrent que l’indice de Fisher n’est pas fortement corrélé avec les productivités moyennes individuelles des facteurs de production.

4.5 Productivité globale des facteurs

• Dans la section précédente, nous avons montré que les indices donnaient sensiblement les mêmes résultats. Nous avons néanmoins choisi en tant qu’indice de productivité globale des facteurs l’indice de Fisher, étant donné qu’il est une moyenne géométrique de l’indice de Paasche et de celui de Laspeyres.

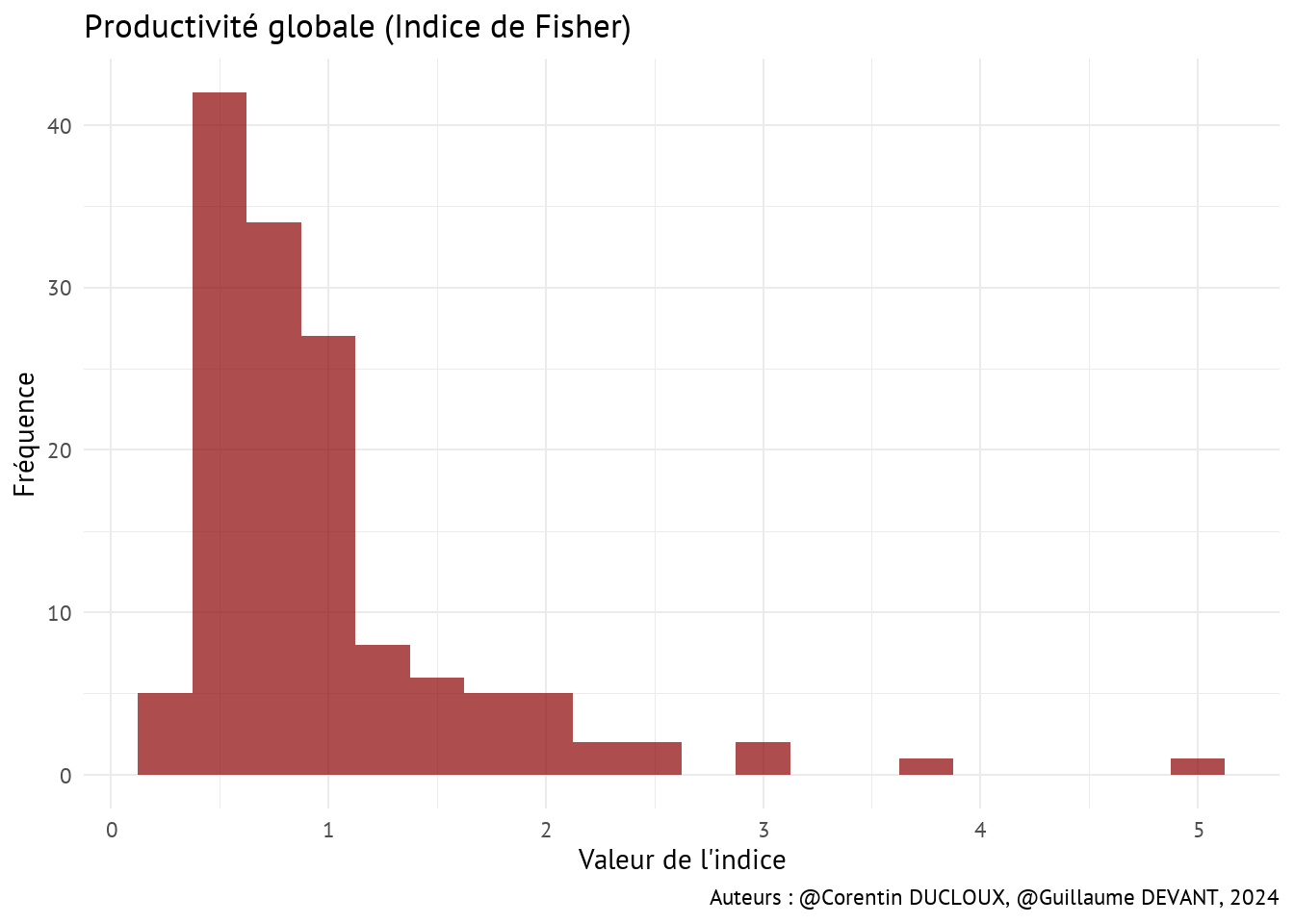
• De manière intéressante, contrairement aux histogrammes des productivités moyennes de la Section 4.1, la plupart des valeurs que prend l’indice de Fisher sont plus concentrées.

Note

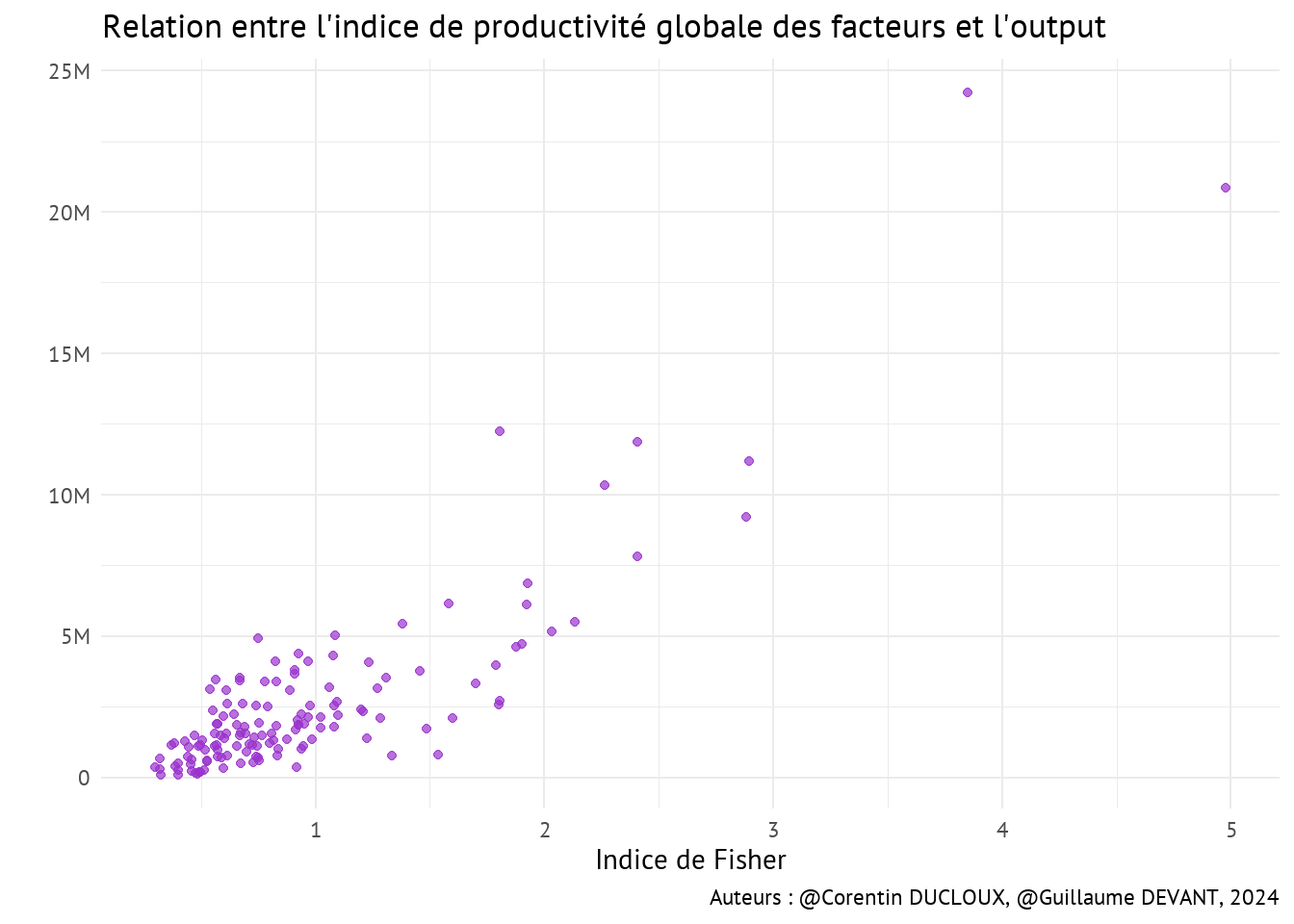
La variable dichotomique adv présente dans notre dataset est définie par :

$$adv=\{\begin{array}{l}0\text{ si le producteur n’est pas conseillé}\\ 1\text{ si le producteur est conseillé}\end{array}$$

On pourrait penser que les producteurs qui ont été conseillés par des laboratoires d’agronomie ont un indice de productivité globale plus important que ceux qui ne l’ont pas été.

Vérifions-le graphiquement et statistiquement

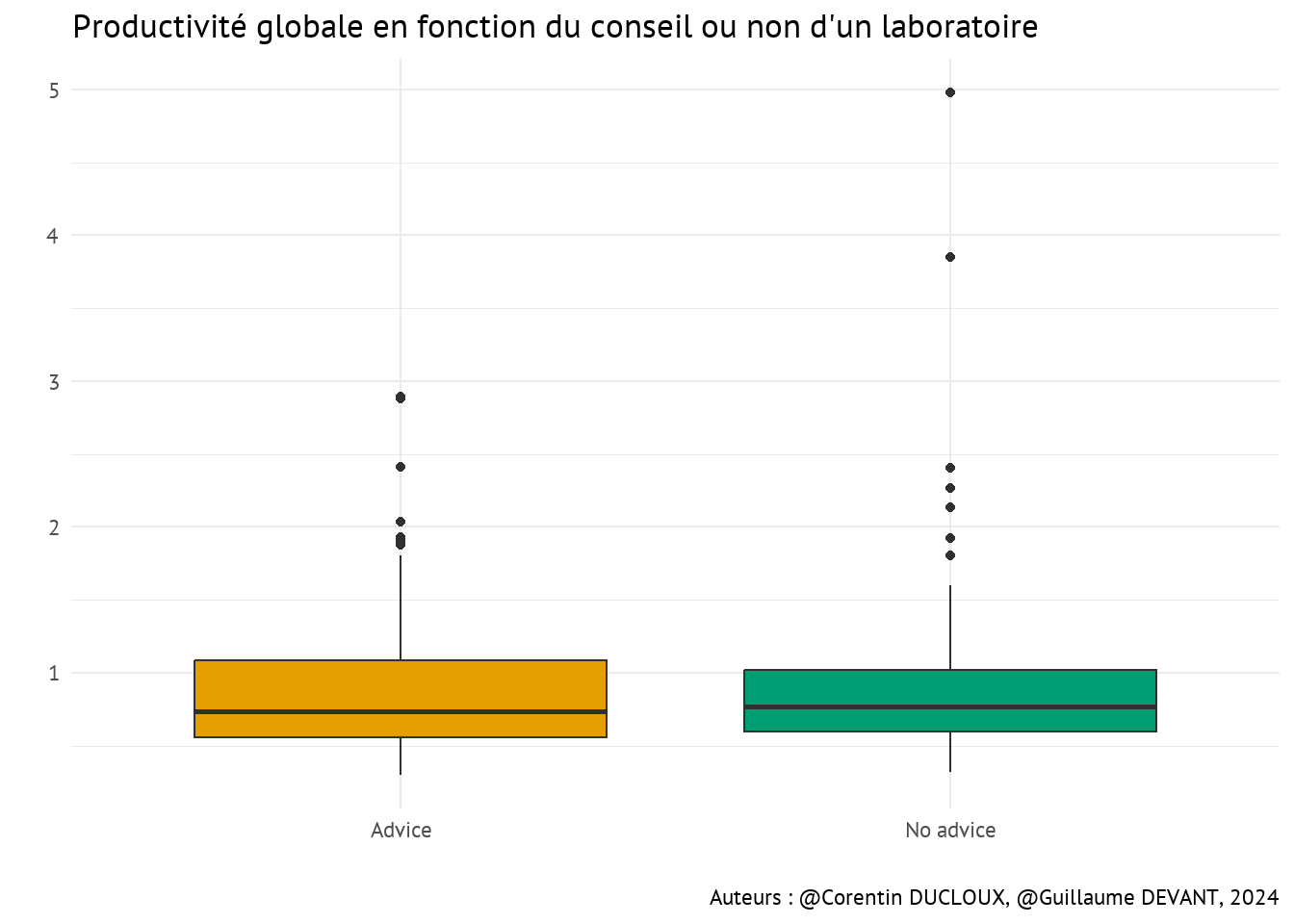
• En moyenne, il semble ne pas y avoir de différence de productivité globale lorsque le producteur est conseillé. En effet, la productivité moyenne avec conseil est égale à 0.95 tandis que la productivité moyenne sans conseil est quant à elle égale à 1.

On peut aussi s’assurer que les moyennes sont significativement différentes en faisant un test de Student bilatéral :

$$\{\begin{array}{l}{H}_0:{\mu }_{advice}={\mu }_{no\mathrm{\_}advice}\\ H_1:{\mu }_{advice}\ne {\mu }_{no\mathrm{\_}advice}\end{array}$$

$\Rightarrow$ Au risque $\alpha =5\mathrm{\%}$, la $p-value$ issue du test est égale à 0.64 $>0.05$, on conserve donc l’hypothèse nulle $H_0$, c’est à dire qu’il n’y a pas de différence significative dans les productivités globales quand le producteur est conseillé/ qu’il ne l’est pas.

5 Analyse exploratoire

5.1 Analyse en composantes principales

L’analyse en composantes principales (ACP) que nous nous apprêtons à faire est justifiée dans notre contexte car nous n’avons que des variables numériques.

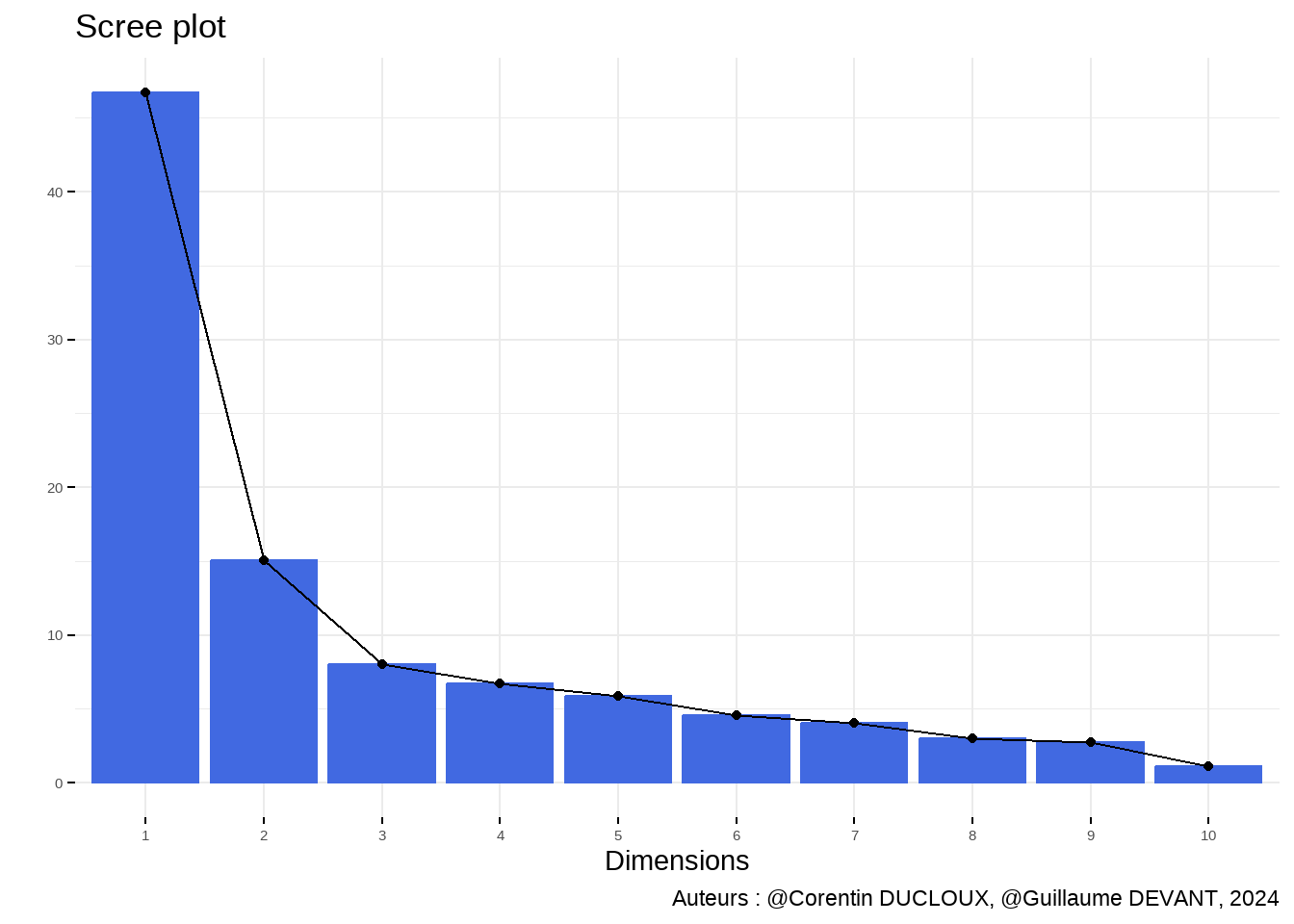
Les deux premiers axes concentrent 60% de la variance. Nous allons dès lors limiter notre ACP à l’étude de ces axes.

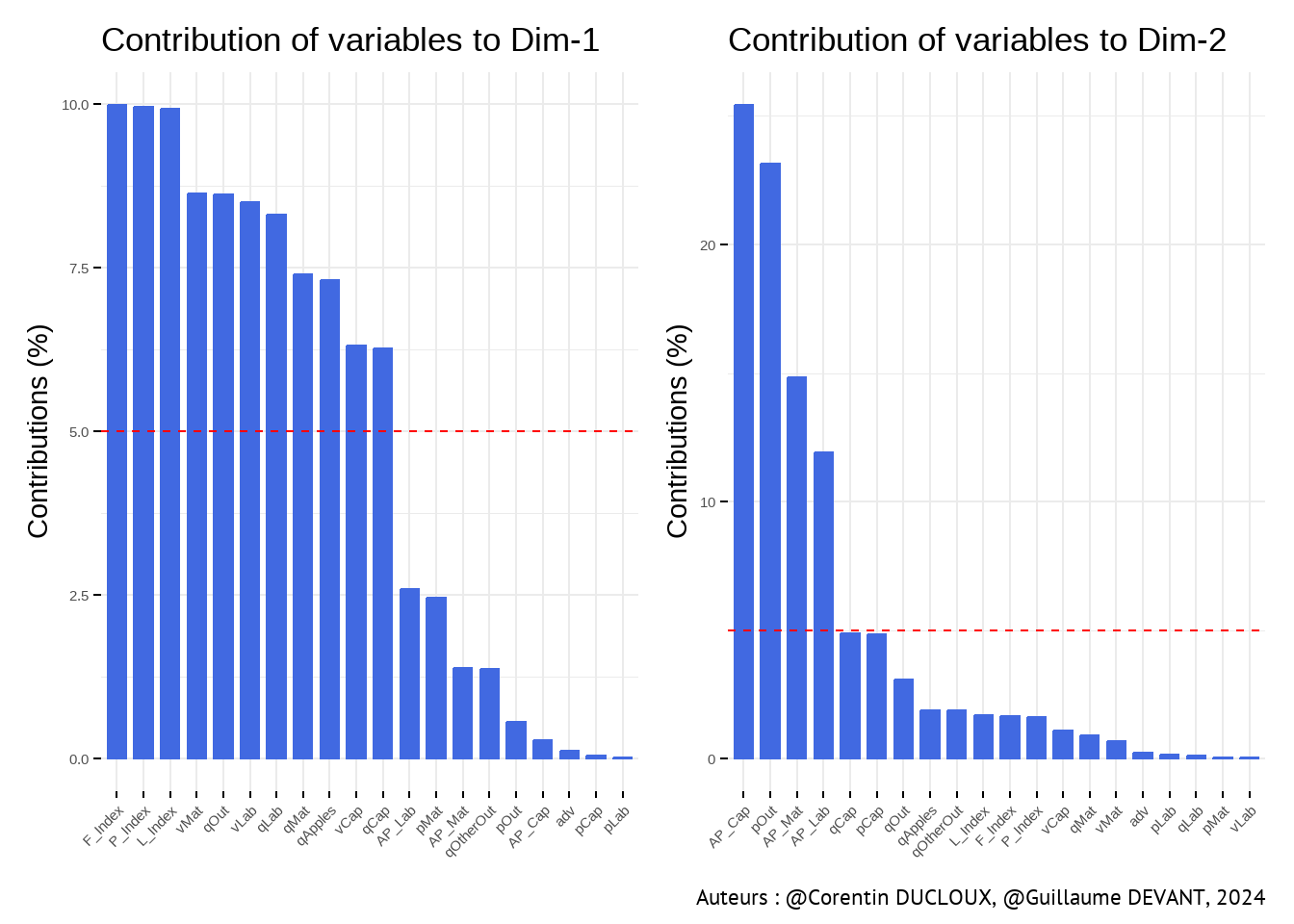
• Axe 1 $\Rightarrow$ Combinaison de variables : synthéthise les indices de Fisher, Paasche et Laspeyres (F_Index, P_Index, L_Index), ainsi que les quantités (qOut, qLab, qCap, qMat) et les coûts des 3 facteurs de production (vMat, vLab, vCap).

• Axe 2 $\Rightarrow$ Productivités moyennes (AP_Cap,AP_Mat,AP_Lab) et prix de vente de la production (pOut)

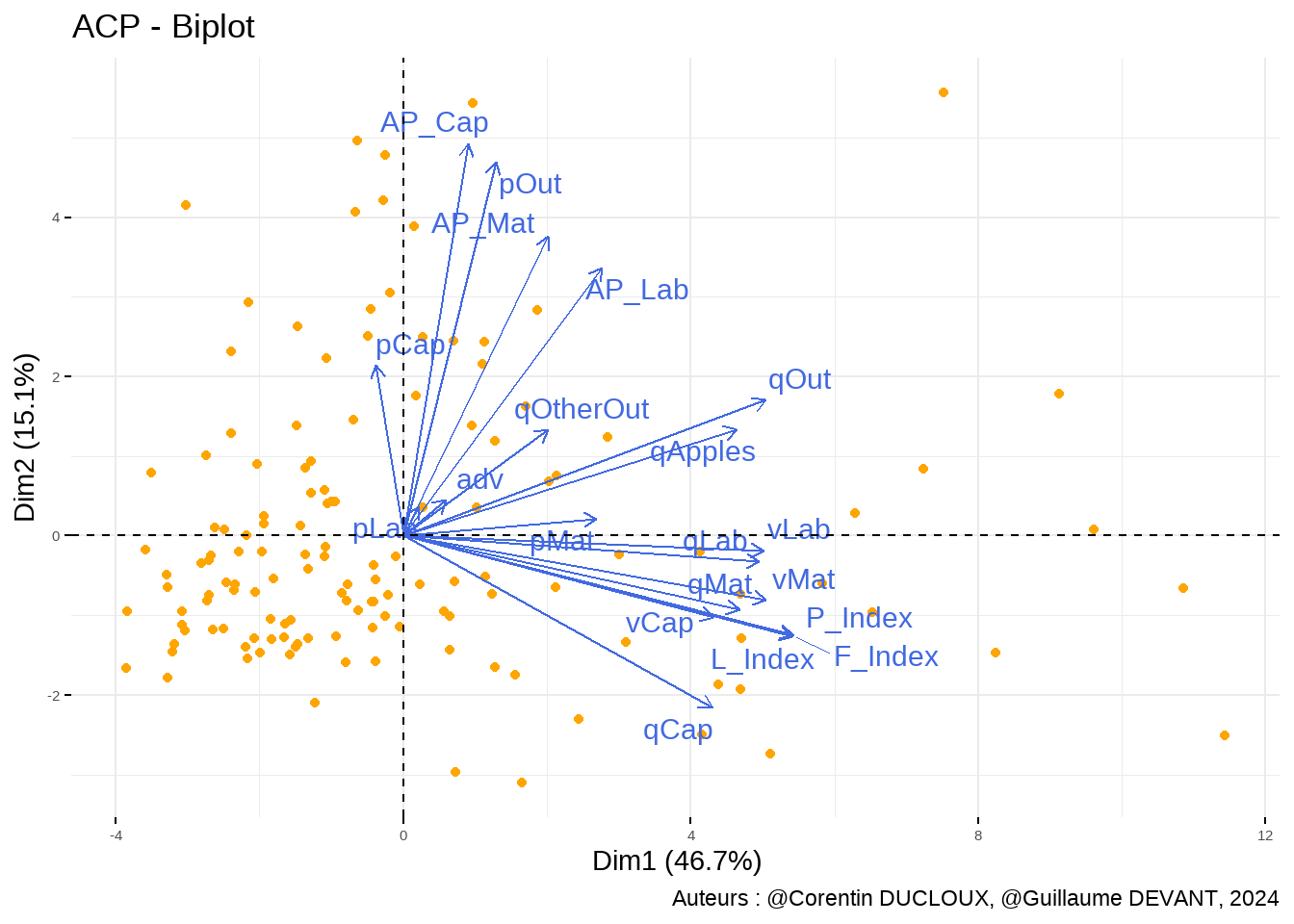
Dans notre ACP, on ne constate pas de variables qui sont fortement opposées. Elle permet néanmoins de mettre en avant le lien entre les quantités des facteurs de production et leur valeur. On observe également que le prix de vente est étroitement lié avec les productivités moyennes.

5.2 Bonus : La répartition de qOut

Lorsque l’on s’intéresse à la distribution de qOut et que l’on met ces valeurs en logarithme, on remarque une distribution proche d’une loi normale. Cette observation est confirmée par le test de Shapiro effectué ci-dessous.

$$\{\begin{array}{l}{H}_0:\ln (q_{Out})\text{ suit une distribution normale}\\ H_1:\ln (q_{Out})\text{ ne suit pas une distribution normale}\end{array}$$

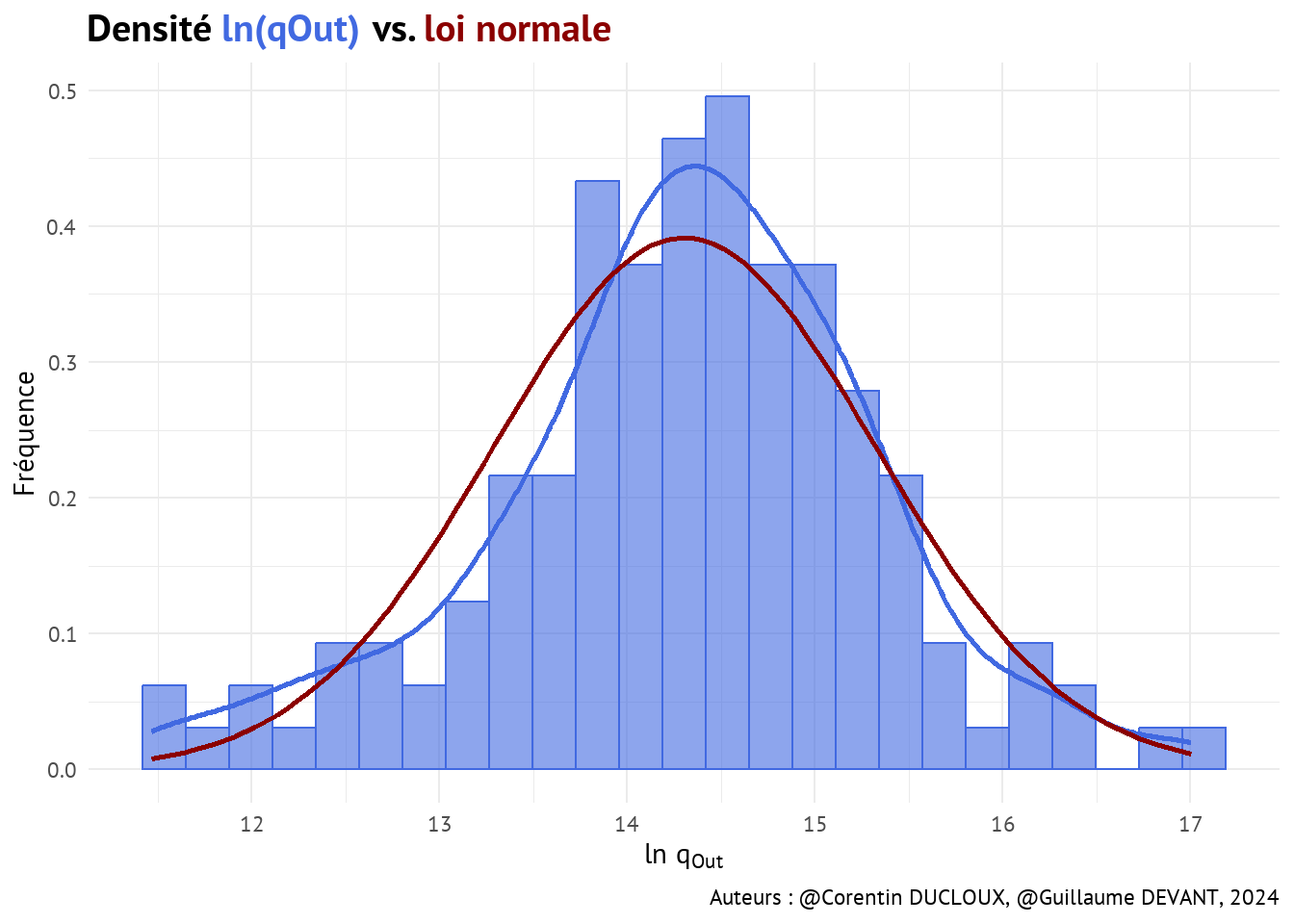
$\Rightarrow$ Au seuil $\alpha =5\mathrm{\%}$, le test de Shapiro confirme statistiquement le fait que les données ln(qOut) suivent une distribution normale avec une $p-value$ = 0.11 soit $>0.05$, donc $H_0$ n’est pas rejeté.

6 Fonctions de production

Une fonction de production représente la relation entre les quantités des différents facteurs de production utilisés (ici qCap, qLab, qMat) et la quantité de production obtenue (ici qOut).

6.1 Fonction de production linéaire

Forme de la fonction

$$q_i=\alpha +\sum _{k=1}^3{\beta }_k{x}_{ik}+{\epsilon }_i$$

• La fonction de production linéaire dans notre cas s’écrit donc sous la forme :

$$q_{Out}=\alpha +{\beta }_1{q}_{Cap}+{\beta }_2{q}_{Lab}+{\beta }_3{q}_{Mat}+{\epsilon }_i$$

On a pu constater un lien indéniable entre la quantité produite (qOut) et les productivités moyennes. On peut alors légitimement penser qu’il existe une relation entre la quantité produite et les quantités des facteurs de production.

Avant de s’aventurer dans des formes fonctionnelles plus complexes, commençons par utiliser une simple fonction de production linéaire.

linreg_prod <- lm(qOut ~ qCap + qLab + qMat, data = apples)

Fonction de production linéaire
Variable dépendante : qOut
	Description	Coefficients	Ecart Type	Pvalues	Significativité
$\alpha$	Constante du modèle	−1,615,978.639	+/- 231771.709	0	$\ast \ast \ast$
${\beta }_1$	Coefficient associé à la variable qCap	1.788	+/- 1.995	0.372
${\beta }_2$	Coefficient associé à la variable qLab	11.831	+/- 1.272	0	$\ast \ast \ast$
${\beta }_3$	Coefficient associé à la variable qMat	46.668	+/- 11.234	0	$\ast \ast \ast$
Observations : 140
$R^2=$ 0.787
$R_{adj}^2=$ 0.782

• Le coefficient associé à qCap est de 1.788, mais il n’est pas statistiquement significatif, ce qui suggère que la quantité de capital n’a pas une influence significative sur la production totale.

• Le coefficient associé à qLab est de 11.831 avec un niveau de significativité très élevé, ce qui signifie que pour chaque unité supplémentaire de travail utilisée, la production totale augmente en moyenne de 11.831 unités, ceteris paribus. Cela revèle une fois de plus l’influence importante de la quantité de travail sur la quantité d’output.

• Le coefficient associé à qMat est de 46.668 avec un niveau de significativité très élevé, ce qui indique que pour chaque unité supplémentaire de matériaux utilisés, la production totale augmente en moyenne de 46.668 unités, ceteris paribus.

$R_{adj}^2=$ 0.782 donc 78.2% de la variance de la production totale est expliquée par la variance des variables explicatives.

🔎 Comparaison de la production effective et de la production prédite

\(q_{Out}\)

\(\widehat{q_{Out}}\)

\(\varepsilon_i\)

\(\widehat{q_{Out}}/q_{Out}\)

350K

−150K

500K

−0.43

1.1M

20K

1.1M

0.018

1.1M

190K

930K

0.17

1.1M

190K

880K

0.18

3.1M

710K

2.4M

0.23

1.5M

330K

1.1M

0.23

3.4M

850K

2.6M

0.25

680K

170K

510K

0.25

1.3M

350K

970K

0.26

3.4M

1.0M

2.4M

0.30

1–10 of 140 rows

...

La multicolinéarité est un problème qui survient lorsque certaines variables explicatives du modèle mesurent le même phénomène.

Une multicolinéarité importante peut s’avérer problématique, car elle peut augmenter la variance des coefficients de régression et ainsi les rendre instables.

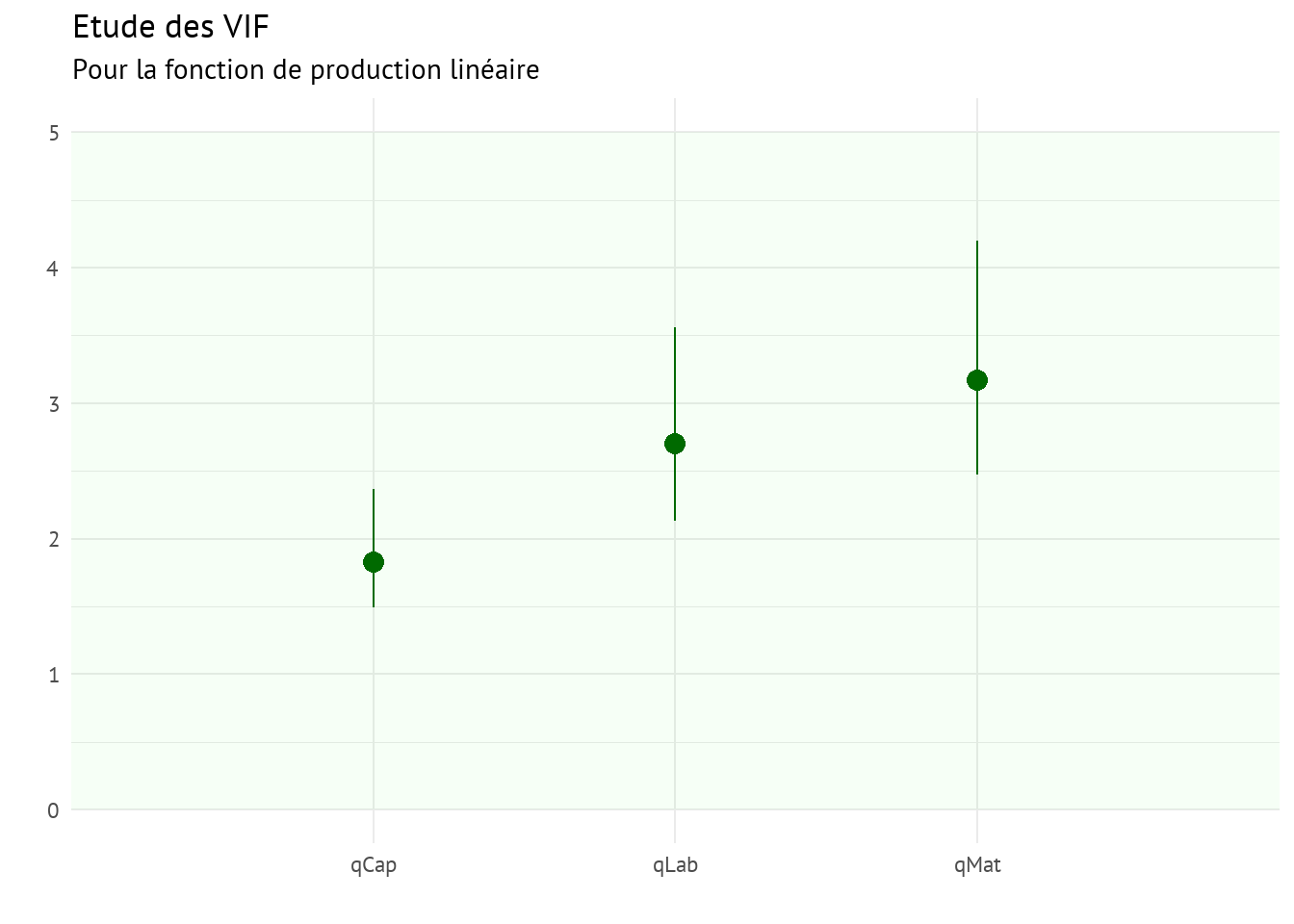
Les VIF (Variance Inflation Factor) estiment de combien la variance d’un coefficient est augmentée en raison d’une relation linéaire avec d’autres prédicteurs.

• Ici, les VIF sont faibles $(<5)$, il n’y a donc pas de raison de s’inquiéter concernant une éventuelle multicolinéarité

6.1.1 Spécification de la forme fonctionnelle

On peut utiliser un RESET test pour vérifier si la forme fonctionnelle linéaire est la bonne spécification.

$$\{\begin{array}{l}{H}_0:\text{La relation entre la variable a predire et un ou plusieurs predicteurs est lineaire}\\ H_1:\text{La relation entre la variable a predire et un ou plusieurs predicteurs est quadratique}\end{array}$$

$\Rightarrow$ Au risque $\alpha =5\mathrm{\%}$, la $p-value$ issue du test est $<0.05$, on rejette donc l’hypothèse nulle $H_0$, c’est à dire qu’on va préférer prendre une forme fonctionnelle incluant des effets quadratiques.

Inconvénients de la forme fonctionnelle linéaire

Malgré un $R_{adj}^2$ proche de 0.8, ce qui signifie que le modèle a plutôt un bon ajustement, la spécification linéaire possède plusieurs problèmes :

1. Les rendements d’échelle sont fixés comme constants dans la forme fonctionnelle.
2. Elle ne permet pas d’évaluer les possibilités de substitution entre les trois facteurs de production.

$\Rightarrow$ Face à ces inconvénients du modèle linéaire, la fonction Cobb-Douglas permet de fournir une réponse au point (1).

6.2 Fonction de production Cobb-Douglas

Forme de la fonction

$$q_i=A\prod _{k=1}^3{x}_{ik}^{a_k}{\epsilon }_i$$

• La fonction de production Cobb-Douglas dans notre cas s’écrit donc sous la forme :

$$q_{Out}=A\cdot q_{Cap}^{\alpha }\cdot q_{Lab}^{\beta }\cdot q_{Mat}^{\gamma }\cdot {\epsilon }_i$$

On peut aussi facilement linéariser la fonction pour pouvoir la préparer à une procédure lm, dès lors on obtient :

$$\ln (q_{out})=\ln (A)+\alpha \cdot \ln (q_{Cap})+\beta \cdot \ln (q_{Lab})+\gamma \cdot \ln (q_{Mat})+\ln ({\epsilon }_i)$$

Le package micEcon propose néanmoins l’estimation d’une fonction de production Cobb-Douglas grâce à la fonction translogEst et l’argument linear = TRUE¹.

cd_prod <- translogEst(
    "qOut",
    c("qCap", "qLab", "qMat"),
    data = apples,
    linear = TRUE
)

Fonction de production Cobb-Douglas
Variable dépendante : ln(qOut)
	Description	Coefficients	Ecart Type	Pvalues	Significativité
$A$	Constante du modèle	−2.064	+/- 1.313	0.118
$\alpha$	Coefficient associé à la variable ln(qCap)	0.163	+/- 0.087	0.064	$\ast$
$\beta$	Coefficient associé à la variable ln(qLab)	0.676	+/- 0.154	0	$\ast \ast \ast$
$\gamma$	Coefficient associé à la variable ln(qMat)	0.627	+/- 0.126	0	$\ast \ast \ast$
Observations : 140
$R^2=$ 0.594
$R_{adj}^2=$ 0.585

Dans le cadre de cette régression, étant donné que le modèle est sous forme $\log -\log$, on peut interpréter les 3 coefficients comme des élasticités partielles :

• $\alpha \Rightarrow$ Un changement d’un pourcent de qCap induit un changement de 0.163% de qOut, ceteris paribus.

• $\beta \Rightarrow$ Un changement d’un pourcent de qLab induit un changement de 0.676% de qOut, ceteris paribus.

• $\gamma \Rightarrow$ Un changement d’un pourcent de qMat induit un changement de 0.627% de qOut, ceteris paribus.

Note : les coefficients sont significatifs au seuil de 10% pour qCap, 1% pour qLab et 1% pour qMat.

• Le $R_{adj}^2=$ 0.585. On ne peut cependant pas directement comparer les $R_{adj}^2$ entre les fonctions de production linéaires et Cobb-Douglas puisque les variables dépendantes ne sont pas les mêmes.

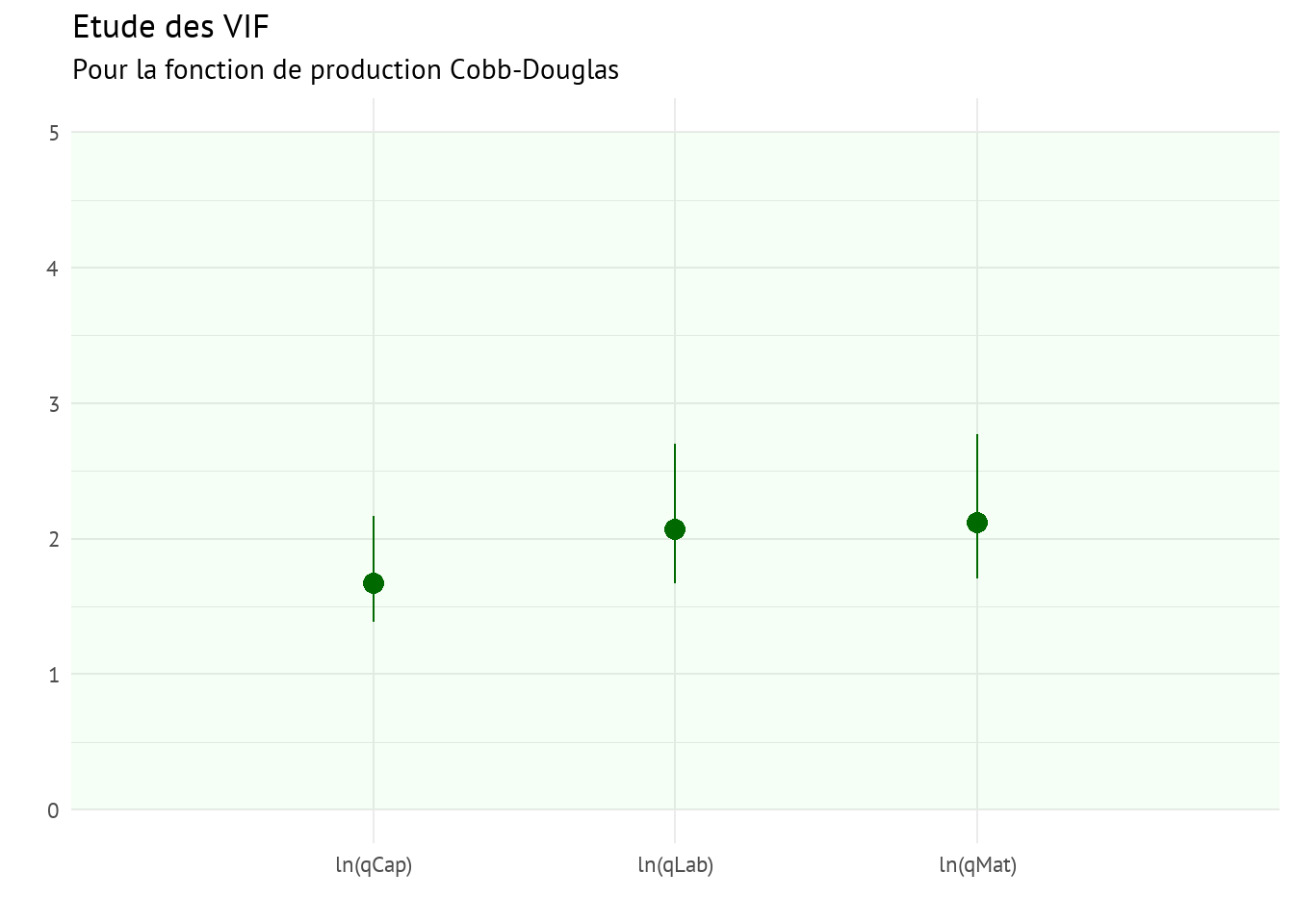
Comme dans la fonction de production linéaire, il ne semble pas y avoir de problème de multicolinéarité ici.

6.2.1 Rendements d’échelle

On l’a vu ci-dessus, les exposants $\alpha$, $\beta$ et $\gamma$ sont les élasticités de la production, c’est-à-dire qu’ils mesurent respectivement le changement en pourcentage de l’output aux variations en pourcentage de la quantité de capital, de la quantité de travail et de la quantité de matériaux.

• Grâce à ces coefficients estimés, on peut déterminer les rendements d’échelle.

Note sur les rendements d’échelle

• Décroissants si $\hat{\alpha }+\hat{\beta }+\hat{\gamma }<1$

• Constants si $\hat{\alpha }+\hat{\beta }+\hat{\gamma }=1$

• Croissants si $\hat{\alpha }+\hat{\beta }+\hat{\gamma }>1$

alpha <- cd_prod$coef[2] |> unname()
beta <- cd_prod$coef[3] |> unname()
gamma <- cd_prod$coef[4] |> unname()

return_to_scale <- alpha + beta + gamma

• On trouve que $\hat{\alpha }+\hat{\beta }+\hat{\gamma }=$ 1.47, donc les rendements d’échelles sont croissants, c’est à dire que le processus de production présente des économies d’échelle. Un accroissement identique de tous les facteurs conduit à un accroissement plus important de la production.

• Ces rendements d’échelle croissants sont souvent le résultat de coûts fixes élevés (voir la Section 3.1 pour s’en convaincre).

Une implication de ce résultat est que des installations de production à grande échelle ont tendance à être plus efficaces que des installations à petite échelle.

---

Intéressons-nous à l’élasticité de substitution, qui mesure la facilité avec laquelle un input peut être substitué par un autre.

• Si l’elasticité de substitution n’est pas empiriquement estimable pour la Cobb-Douglas, celle-ci suppose implicitement que l’élasticité de substitution de Allen est égale à un, soit ${\sigma }_{\{\text{qCap, qLab, qMat}\}}=1$.

• Cela implique une substitution parfaite entre les facteurs de production $q_{Cap}$, $q_{Lab}$ et $q_{Mat}$, ce qui va clairement à l’encontre des résultats de la Section 4.1.

6.2.2 Productivité marginale des inputs

La productivité marginale se réfère à la variation de la production totale résultant d’une petite variation d’un facteur de production spécifique, toutes choses égales par ailleurs.

En d’autres termes, il s’agit de la quantité supplémentaire d’output qu’une entreprise peut produire en utilisant une unité supplémentaire d’un facteur de production donné, tout en maintenant constantes les quantités des autres facteurs de production.

Nous obtenons alors respectivement :

• $M{P}_{Cap}=\frac{\partial q_{Out}}{\partial q_{Cap}}$

• $M{P}_{Lab}=\frac{\partial q_{Out}}{\partial q_{Lab}}$

• $M{P}_{Mat}=\frac{\partial q_{Out}}{\partial q_{Mat}}$

On peut facilement calculer ces productivités marginales avec la fonction cobbDouglasDeriv.

cd_prod_margProducts <- cobbDouglasDeriv(
    c("qCap", "qLab", "qMat"),
    data = apples, coef = coef(cd_prod)[1:4],
    coefCov = vcov(cd_prod)[1:4, 1:4]
)

Productivités marginales

Dans le cadre d’une fonction de production Cobb-Douglas

\(N\)

\(MP_{Cap}\)

\(MP_{Lab}\)

\(MP_{Mat}\)

Producteur 1

6.23

6.03

59.09

Producteur 2

10.21

6.73

38.17

Producteur 3

5.28

5.78

31.05

Producteur 4

5.06

5.34

21.89

Producteur 5

2.40

4.98

28.60

Producteur 6

8.82

7.95

67.23

Producteur 7

4.10

9.22

32.41

Producteur 8

3.57

5.87

48.38

Producteur 9

10.05

6.26

30.44

Producteur 10

2.38

4.24

59.61

1–10 of 140 rows

...

• Par exemple, pour le producteur 1 :
  • L’augmentation d’une unité de capital tout en maintenant constant le niveau de travail et de matériaux entraînera une augmentation de 6.23 unités d’output.
  • L’augmentation d’une unité de travail tout en maintenant constant le niveau de capital et de matériaux entrainera une augmentation de 6.03 unités d’output.
  • L’augmentation d’une unité de matériaux tout en maintenant constant le niveau de travail et de capital entrainera une augmentation de 59.09 unités d’output.

On remarque dans ce modèle que la productivité marginale des matériaux est supérieure à celle du capital et du travail pour tous les producteurs. De plus, aucune productivité marginale n’est négative, c’est à dire que rajouter des quantités de n’importe quel input sans augmenter les autres résultera toujours en une augmentation de la production.

6.3 Fonction de production quadratique

Forme de la fonction

$$q_i=\alpha +\sum _{k=1}^3{\beta }_k{x}_{ik}+\frac{1}{2}\sum _{l=1}^3\sum _{k=1}^3{\beta }_{kl}{x}_{ik}{x}_{il}+{\epsilon }_i$$

• La fonction de production quadratique dans notre cas s’écrit donc sous la forme :

$$\begin{array}{c}{q}_{Out}=\alpha +{\beta }_1{q}_{Cap}+{\beta }_2{q}_{Lab}+{\beta }_3{q}_{Mat}\\ +\frac{1}{2}({\beta }_{11}{q}_{Cap}^2+{\beta }_{22}{q}_{Lab}^2+{\beta }_{33}{q}_{Mat}^2)\\ +{\beta }_{12}{q}_{Cap}{q}_{Lab}+{\beta }_{13}{q}_{Cap}{q}_{Mat}+{\beta }_{23}{q}_{Lab}{q}_{Mat}+{\epsilon }_i\end{array}$$

✅ Avantages :

• La fonction de production quadratique va permettre d’ajouter des termes quadratiques et des effets d’interaction, rendant la modélisation plus robuste.

❌ Inconvénients :

• L’ajout de termes supplémentaires implique plus de complexité et de coefficients à estimer $(3^2=9)$.

quad_prod <- quadFuncEst(
    "qOut",
    c("qCap", "qLab", "qMat"),
    data = apples
)

Fonction de production quadratique
Variable dépendante : qOut
	Description	Coefficients	Ecart Type	Pvalues	Significativité
$\alpha$	Constante du modèle	−291,113.132	+/- 361461.083	0.422
${\beta }_1$	Coefficient associé à la variable qCap	5.27	+/- 4.403	0.234
${\beta }_2$	Coefficient associé à la variable qLab	6.077	+/- 3.185	0.059	$\ast$
${\beta }_3$	Coefficient associé à la variable qMat	14.303	+/- 24.057	0.553
${\beta }_{11}$	Coefficient associé à la variable qCap²	0.00005	+/- 0	0.176
${\beta }_{12}$	Coefficient associé à la variable qCap×qLab	−0.00003	+/- 0	0.041	$\ast \ast$
${\beta }_{13}$	Coefficient associé à la variable qCap×qMat	−0.00004	+/- 0	0.778
${\beta }_{22}$	Coefficient associé à la variable qLab²	−0.00003	+/- 0	0.141
${\beta }_{23}$	Coefficient associé à la variable qLab×qMat	0.0004	+/- 0	0	$\ast \ast \ast$
${\beta }_{33}$	Coefficient associé à la variable qMat²	−0.002	+/- 0.001	0.036	$\ast \ast$
Observations : 140
$R^2=$ 0.845
$R_{adj}^2=$ 0.834

• Le coefficient associé à qCap est de 5.27, mais il n’est pas statistiquement significatif, ce qui suggère que la quantité de capital n’a pas une influence significative sur la production totale dans ce modèle.

• Le coefficient associé à qLab est de 6.077 avec un niveau de significativité assez faible, ce qui signifie que pour chaque unité supplémentaire de travail utilisée, la production totale augmente en moyenne de 6.077 unités, toutes choses égales par ailleurs.

• Le coefficient associé à qMat est de 14.303, mais il n’est pas statistiquement significatif, ce qui suggère que la quantité de matériaux n’a pas une influence significative sur la production totale dans ce modèle.

• Le coefficient associé à l’effet d’interaction entre les quantités de capital et de travail (qCap×qLab) est négatif et significatif au seuil de 5%. Cela suggère que l’interaction entre ces 2 facteurs a un effet négatif sur la production.

• Le coefficient associé à l’effet d’interaction entre les quantités de tavail et de matériaux (qLab×qMat) est positif et significatif au seuil de 1%. Cela suggère que l’interaction entre ces 2 facteurs a un effet positif sur la production.

• Enfin, le coefficient associé à l’effet quadratique des matériaux (qMat²) est statistiquement significatif au seuil 5% et possède une valeur négative, ce qui suggère une courbe de rendement d’échelle décroissante pour les matériaux, indiquant que l’augmentation de la quantité de matériaux pourrait initialement augmenter la production, mais à un rythme décroissant.

$R_{adj}^2=$ 0.834 donc 83.4% de la variance de la production totale est expliquée par la variance des variables explicatives. Ce résultat est meilleur que la fonction de production linéaire.

🔎 Comparaison de la production effective et de la production prédite

\(q_{Out}\)

\(\widehat{q_{Out}}\)

\(\varepsilon_i\)

\(\widehat{q_{Out}}/q_{Out}\)

3.1M

1.1M

2.0M

0.36

3.4M

1.2M

2.2M

0.36

3.1M

1.2M

1.9M

0.38

4.9M

1.9M

3.0M

0.39

3.4M

1.5M

2.0M

0.43

4.1M

1.8M

2.3M

0.44

4.4M

2.1M

2.3M

0.48

4.3M

2.1M

2.2M

0.49

4.1M

2.1M

2.0M

0.51

3.4M

1.8M

1.6M

0.52

1–10 of 140 rows

...

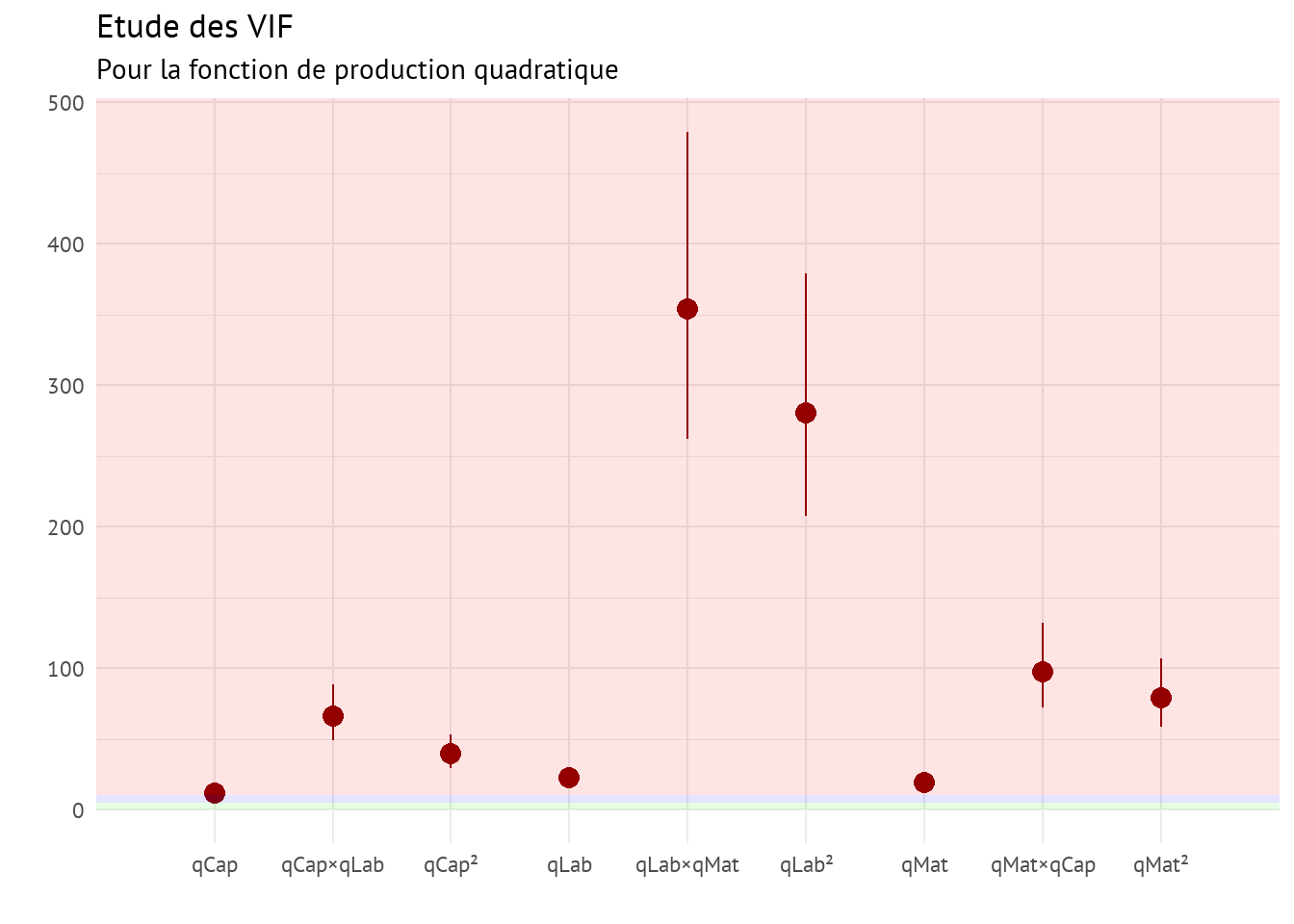
Les valeurs de VIF sont ici extrêmement élevées. La forme fonctionnelle du modèle avec interactions et effets quadratiques entraîne naturellement ces forts problèmes de multicolinéarité.

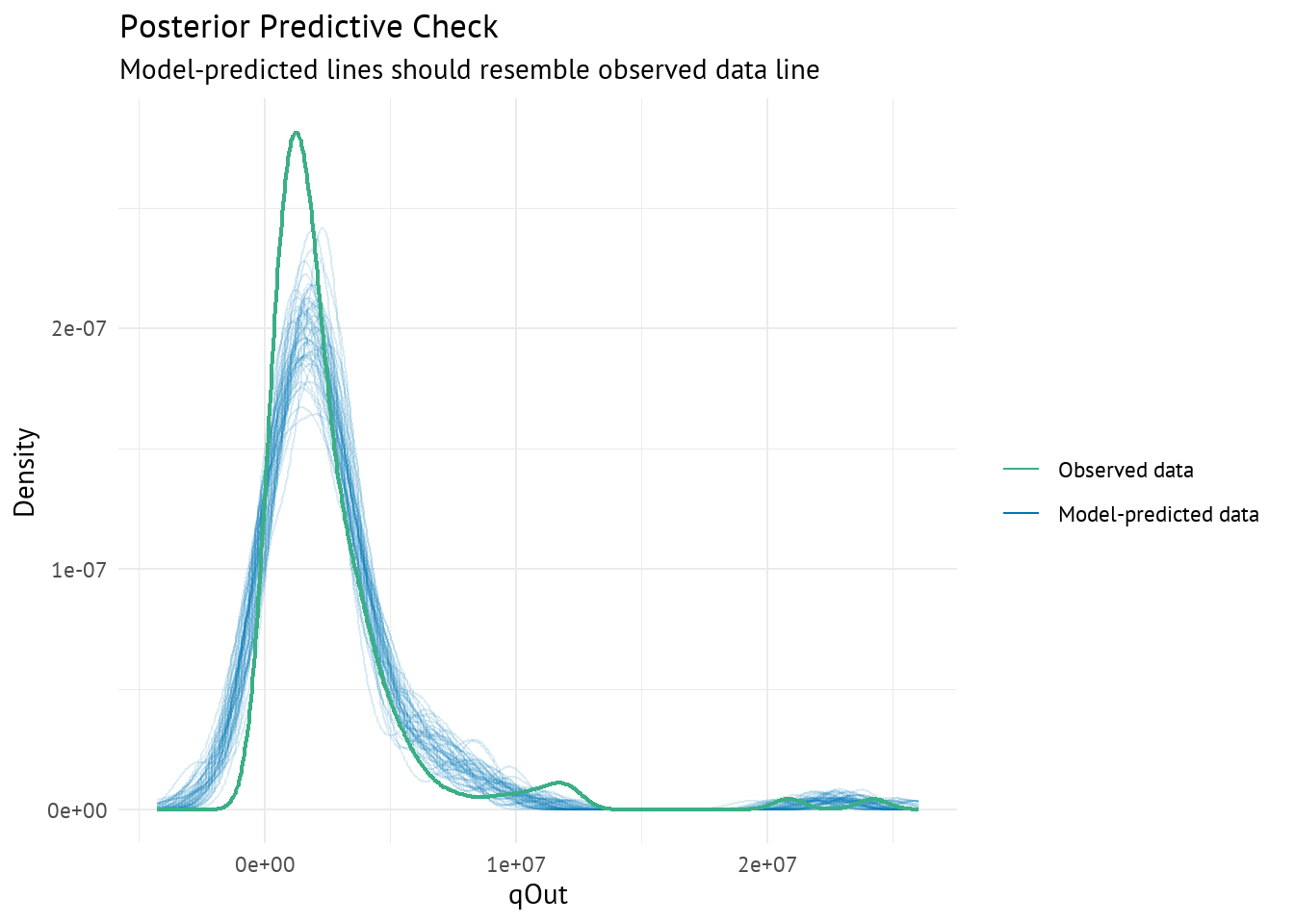
On semble être dans une situation de surapprentissage, en effet le modèle s’ajuste trop par rapport aux données sur lesquelles il a été entrainé, il généralise donc mal et est très sensible au bruit.

6.3.1 Productivité marginale des inputs

quad_prod_margProducts <- quadFuncDeriv(
    c("qCap", "qLab", "qMat"),
    data = apples,
    coef = coef(quad_prod),
    coefCov = vcov(quad_prod)
)

Productivités marginales

Dans le cadre d’une fonction de production quadratique

\(N\)

\(MP_{Cap}\)

\(MP_{Lab}\)

\(MP_{Mat}\)

Producteur 1

−3.07

6.04

90.63

Producteur 2

−2.17

13.52

35.47

Producteur 3

1.78

10.32

23.13

Producteur 4

2.97

10.43

11.08

Producteur 5

4.16

7.73

20.90

Producteur 6

−8.20

9.60

115.17

Producteur 7

2.81

15.85

−6.12

Producteur 8

1.75

6.53

52.68

Producteur 9

−0.29

13.36

20.21

Producteur 10

2.59

2.15

71.66

1–10 of 140 rows

...

Cette fois on remarque qu’il existe des productivités marginales négatives. Prenons l’exemple du producteur 1. Si celui-ci décide d’ajouter une unité de capital en maintenant les autres inputs constants (travail et matériaux), alors sa production va diminuer de 3.07 unités.

6.4 Fonction de production Translog

Forme de la fonction

$$\begin{array}{c}\ln (q_i)=\alpha +\sum _{k=1}^3{\beta }_k\ln (x_{ik})\\ +\frac{1}{2}\sum _{l=1}^3\sum _{k=1}^3{\beta }_{kl}\ln (x_{ik})ln(x_{il})+{\epsilon }_i\end{array}$$

• La fonction de production Translog dans notre cas s’écrit donc sous la forme :

$$\begin{array}{c}\ln (q_{Out})=\alpha +{\beta }_1\ln (q_{Cap})+{\beta }_2\ln (q_{Lab})+{\beta }_3\ln (q_{Mat})\\ +\frac{1}{2}({\beta }_{11}\ln (q_{Cap}^2)+{\beta }_{22}\ln (q_{Lab}^2)+{\beta }_{33}\ln (q_{Mat}^2))\\ +{\beta }_{12}\ln (q_{Cap}{q}_{Lab})+{\beta }_{13}\ln (q_{Cap}{q}_{Mat})+{\beta }_{23}\ln (q_{Lab}{q}_{Mat})+{\epsilon }_i\end{array}$$

translog_prod <- translogEst(
    "qOut",
    c("qCap", "qLab", "qMat"),
    data = apples
)

Fonction de production Translog
Variable dépendante : ln(qOut)
	Description	Coefficients	Ecart Type	Pvalues	Significativité
$A$	Constante du modèle	−4.146	+/- 21.359	0.846
${\beta }_1$	Coefficient associé à la variable ln(qCap)	−2.307	+/- 2.288	0.315
${\beta }_2$	Coefficient associé à la variable ln(qLab)	1.993	+/- 4.566	0.663
${\beta }_3$	Coefficient associé à la variable ln(qMat)	2.232	+/- 3.763	0.554
${\beta }_{11}$	Coefficient associé à la variable ln(qCap²)	−0.026	+/- 0.208	0.902
${\beta }_{12}$	Coefficient associé à la variable ln(qCap)×ln(qLab)	0.562	+/- 0.291	0.056	$\ast$
${\beta }_{13}$	Coefficient associé à la variable ln(qCap)×ln(qMat)	−0.41	+/- 0.235	0.084	$\ast$
${\beta }_{22}$	Coefficient associé à la variable ln(qLab²)	−1.164	+/- 0.679	0.089	$\ast$
${\beta }_{23}$	Coefficient associé à la variable ln(qLab)×ln(qMat)	0.658	+/- 0.428	0.126
${\beta }_{33}$	Coefficient associé à la variable ln(qMat²)	−0.504	+/- 0.435	0.249
Observations : 140
$R^2=$ 0.63
$R_{adj}^2=$ 0.604

Conséquence : L’estimation par moindres carrés ordinaires d’une forme flexible comme la fonction Translog donne des résultats assez médiocres.

En effet, seulement 3 coefficients sont significatifs au seuil de 10% :

• ln(qCap)×ln(qLab)

• ln(qCap)×ln(qMat)

• ln(qLab²)

• Le $R_{adj}^2$ est un peu plus elevé que celui de la Cobb-Douglas, autour de 0.6.

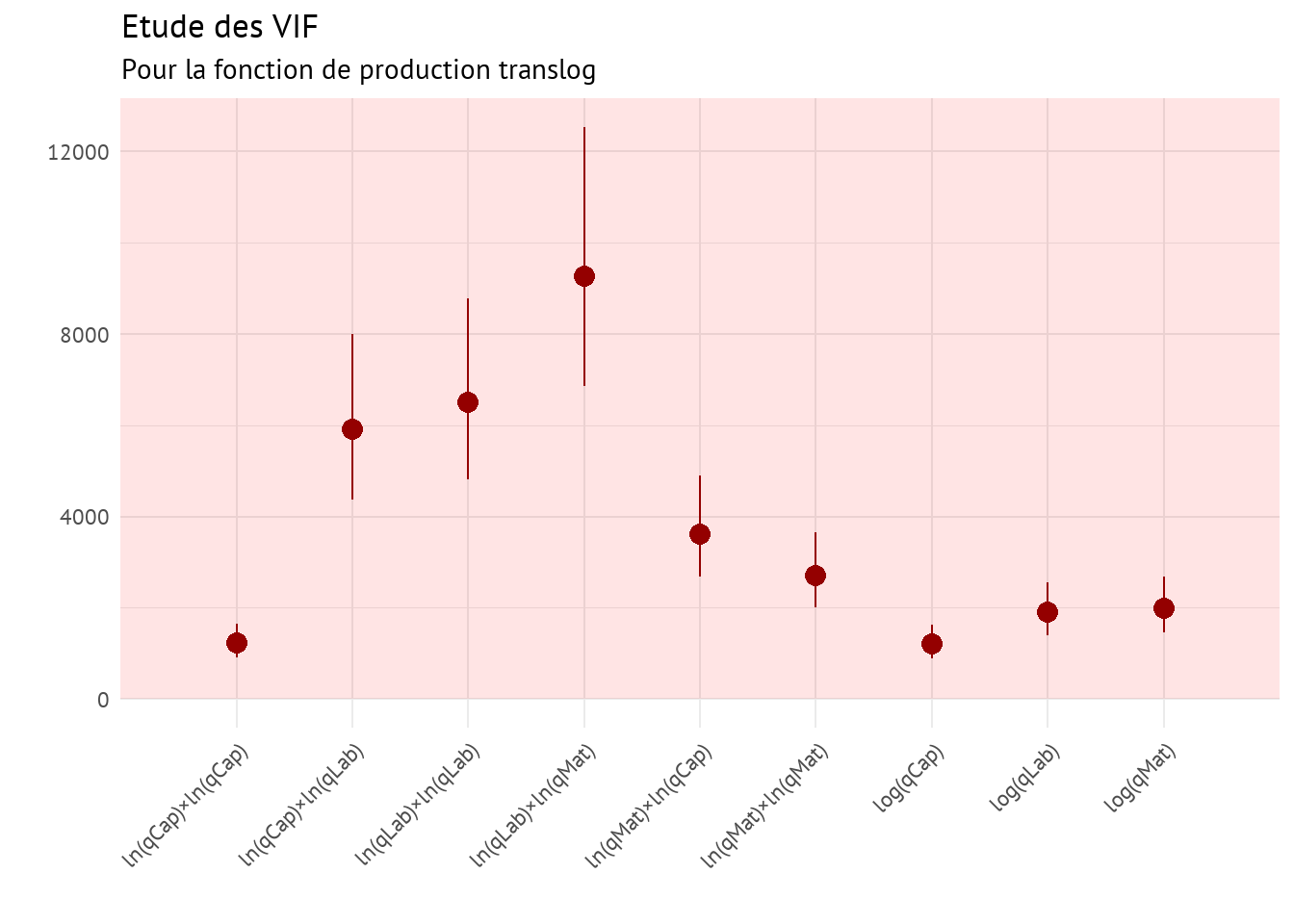
En utilisant une fonction de production Translog, on aggrave considérablement les problèmes de multicolinéarité, rendant les valeurs de VIF encore plus importantes que dans le cas de la fonction de production quadratique.

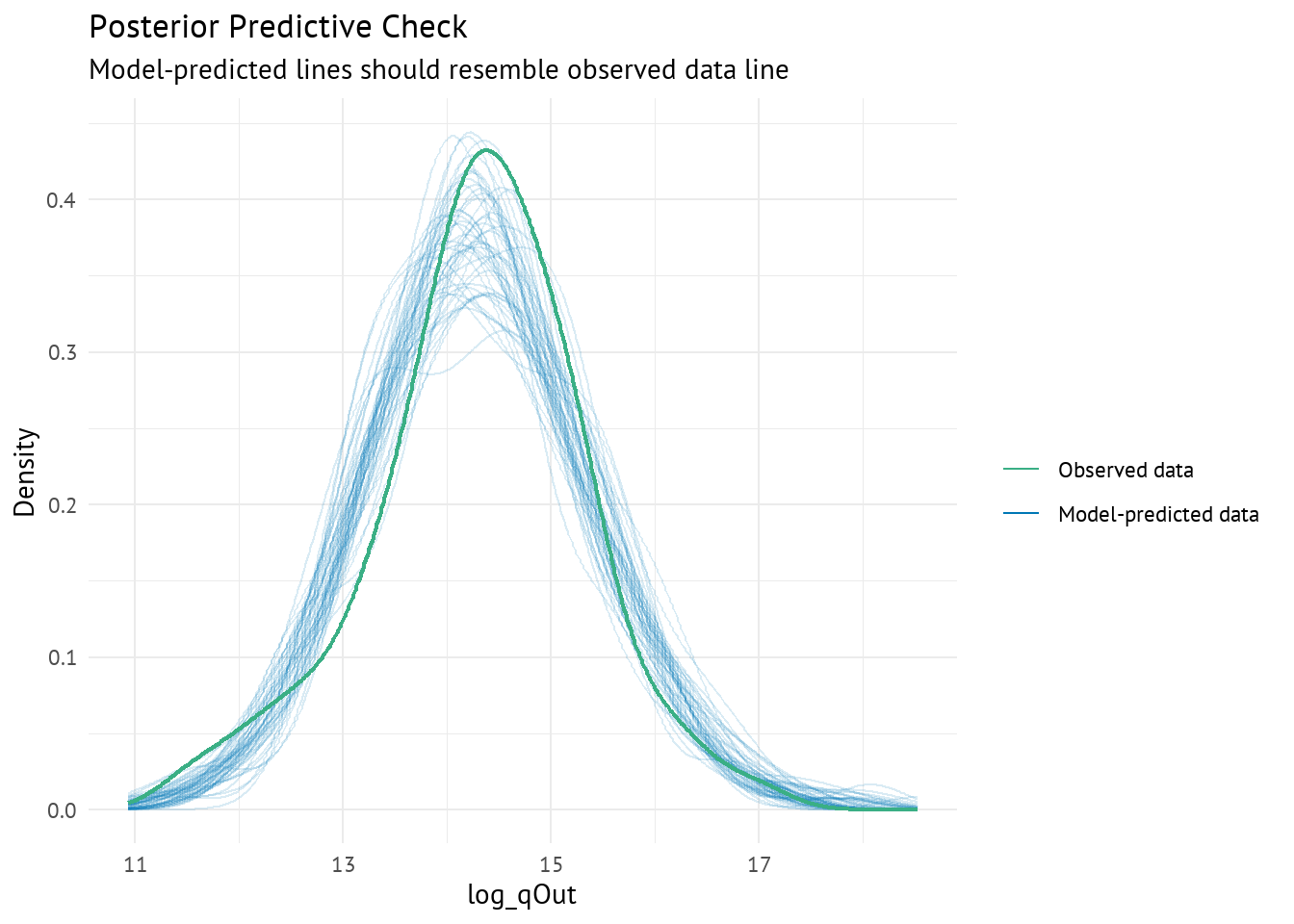
6.4.1 Quel modèle préférer ?

Le test de rapport de vraisemblance est un test d’hypothèse qui compare l’adéquation de l’ajustement de deux modèles afin de déterminer celui qui offre le meilleur ajustement.

Dans notre cas, on veut comparer le modèle Cobb-Douglas et le modèle Translog.

Les hypothèses du test sont les suivantes : $$\{\begin{array}{l}{H}_0:\text{Modele }1\Rightarrow \text{Cobb-Douglas}\\ H_1:\text{Modele }2\Rightarrow \text{Translog}\end{array}$$

La statistique de test est ${\lambda }_{LR}=2\cdot (\ln {\mathcal{L}}_1-\ln {\mathcal{L}}_2)$

• $\ln ({\mathcal{L}}_1)=$ -137.609

• $\ln ({\mathcal{L}}_2)=$ -131.245

$\Rightarrow$ Au risque $\alpha =5\mathrm{\%}$, la $p-value$ issue du test est égale à 0.048 $<0.05$, on rejette donc l’hypothèse nulle $H_0$, c’est à dire que le modèle fonction de production Translog offre un meilleur ajustement.

6.4.2 Coût marginal de la production

Le coût marginal correspond à la fabrication d’une unité supplémentaire d’output (qOut).

La fonction translogProdFuncMargCost nous permet d’estimer ces coûts marginaux dans le cadre d’une fonction de production Translog.

Informations sur les coûts marginaux

• Si le coût marginal est très proche de 0, cela signifie que produire plus ne coûte que très peu cher au producteur. On s’attend donc à ce que les installations qui produisent le plus de pommes aient un coût marginal $\simeq 0$ grâce aux économies d’échelles qu’ils réalisent.

• Si le coût marginal est $<0$, cela signifie que produire moins coûte plus à l’entreprise. Dans ce cas l’entreprise a intérêt à produire plus jusqu’à atteindre un coût marginal proche de 0.

• Si le coût marginal est $>0$, alors il faut que le producteur compare le prix pOut qu’il peut obtenir et son coût marginal pour décider si il doit ou non produire davantage.

margCost <- translogProdFuncMargCost(
    yName = "qOut",
    xNames = c("qCap", "qLab", "qMat"),
    wNames = c("pCap", "pLab", "pMat"),
    data = apples, coef = coef(translog_prod)
)

Coût marginal de la production

Note : Quand $CM>p_{Out}$, la ligne est mise en surbrillance

\(N\)

\(MC\)

\(p_{Out}\)

\(q_{Out}\)

Producteur 1

0.52

0.66

1.37M

Producteur 2

0.31

0.72

1.12M

Producteur 3

0.08

0.94

2.16M

Producteur 4

0.26

0.60

507.39K

Producteur 5

0.13

0.83

1.07M

Producteur 6

0.15

1.39

5.17M

Producteur 7

0.09

1.33

4.30M

Producteur 8

15.74

0.62

1.86M

Producteur 9

0.12

1.91

2.54M

Producteur 10

0.20

0.49

1.20M

1–10 of 140 rows

...

6.4.3 Vérification des conditions de régularité

En premier lieu, on peut vérifier la monotonie de la fonction.

mono <- translogCheckMono(
    c("qCap", "qLab", "qMat"),
    data = apples,
    coef = coef(translog_prod),
    increasing = TRUE
)

$\Rightarrow$ Cette fonction de production Translog augmente de manière monotone dans les facteurs de production qCap, qLab, qMat, dans 65,7% des observations.

---

En second lieu, on peut vérifier si la fonction de production est quasi-concave.

La quasi-concavité garantit que la production réagit de manière décroissante aux augmentations marginales des inputs. Autrement dit, une augmentation marginale d’un input entraîne une augmentation marginale de la production qui décroît au fur et à mesure que cet input augmente.

curv <- translogCheckCurvature(
    c("qCap", "qLab", "qMat"),
    data = apples,
    coef = coef(translog_prod),
    convexity = FALSE,
    quasi = TRUE
)

$\Rightarrow$ Cette fonction de production Translog est quasi-concave dans 45% des observations.

6.5 Fonction de production SFA

Dans le modèle SFA (Stochastic Frontier Analysis), on introduit un terme multiplicatif $T{E}_i$. Ce terme représente l’efficacité technique, définie comme le ratio d’output observé sur l’output maximum réalisable, soit : $T{E}_i=\frac{q_i}{q_i^{\ast }}$.

• On peut ré-écrire ce $T{E}_i$ sous la forme $\exp \{-u_i\}$.

Utiliser un tel modèle va donc nous permettre de pouvoir estimer l’efficacité technique producteur par producteur.

Note : Nous pouvons utiliser plusieurs formes fonctionnelles pour ce modèle, sous la contrainte que notre variable à prédire soit mise sous forme logarithmique, ce qui élimine de facto les modèles de production linéaire et quadratique.

Forme de la fonction

$$q_i=A\prod _{k=1}^3{x}_{ik}^{a_k}\cdot \underset{{\epsilon }_i}{\underbrace{\exp \{-u_i\}\cdot \exp \left\{v_i\right\}}}$$

• La fonction de production SFA Cobb-Douglas dans notre cas s’écrit donc sous la forme :

$$q_{Out}=A\cdot q_{Cap}^{\alpha }\cdot q_{Lab}^{\beta }\cdot q_{Mat}^{\gamma }\cdot \exp \{-u_i\}\cdot \exp \left\{v_i\right\}$$

En linéarisant on obtient :

$$\ln (q_{out})=\ln (A)+\alpha \cdot \ln (q_{Cap})+\beta \cdot \ln (q_{Lab})+\gamma \cdot \ln (q_{Mat})+v_i-u_i$$

cd_sfa <- sfa(log(qOut) ~ log(qCap) + log(qLab) + log(qMat), data = apples)

Fonction de production Cobb-Douglas SFA
Variable dépendante : ln(qOut)
	Description	Coefficients	Ecart Type	Pvalues	Significativité
$A$	Constante du modèle	0.229	+/- 1.25	0.854
$\alpha$	Coefficient associé à la variable ln(qCap)	0.161	+/- 0.08	0.049	$\ast \ast$
$\beta$	Coefficient associé à la variable ln(qLab)	0.685	+/- 0.15	0.000	$\ast \ast \ast$
$\gamma$	Coefficient associé à la variable ln(qMat)	0.466	+/- 0.13	0.000	$\ast \ast \ast$
Observations : 140
Log-Vraisemblance $=$ -133.889
Efficacité moyenne $=$ 0.538

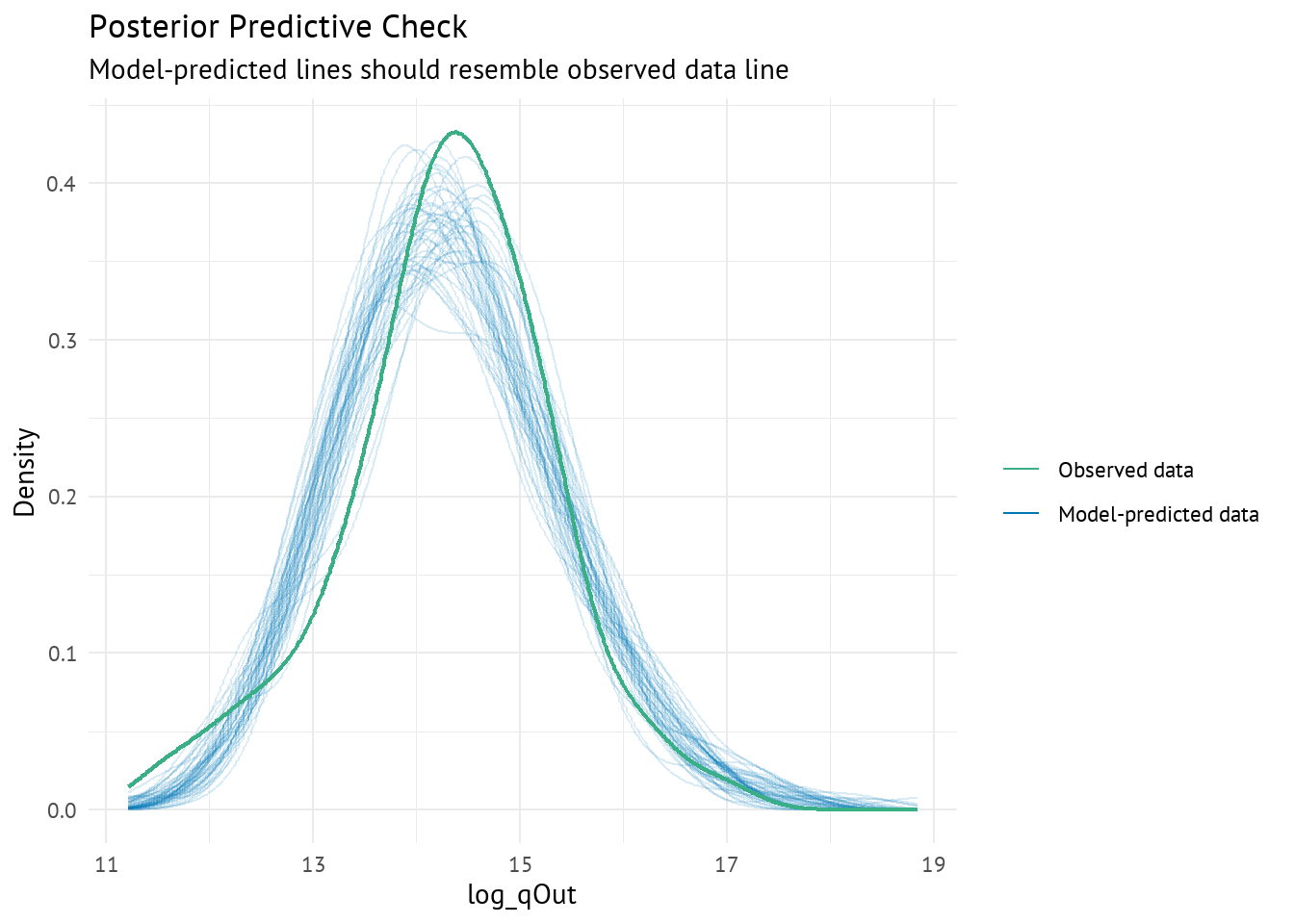
• On remarque que les coefficients et les niveaux de significativité trouvés par l’estimateur du maximum de vraisemblance sont très proches de ceux de la Cobb-Douglas estimés par OLS dans la Section 6.2.

Enfin, les rendements d’échelle sont ici égaux à 1.31, soit un peu moins que ceux trouvés par la fonction de production Cobb-Douglas estimée par MCO.

6.5.1 Analyse de l’efficacité technique des producteurs

L’efficacité technique moyenne des 140 producteurs est de 0.538, c’est à dire qu’il y a certainement un nombre important de producteurs “inefficients”.

En utilisant l’espérance conditionnelle $E(\exp (u_i)|{ϵ}_i)$, on peut estimer le score d’efficacité pour chaque observation. Dans ce cas, les estimations d’efficacité ont des valeurs comprises entre zéro et un, où un indique que le producteur de pommes est pleinement efficace dans sa production et zéro indique que le producteur est totalement inefficace.

efficiencies <- efficiencies(cd_sfa) |> as_tibble()

Producteur le moins/plus efficace
	$TE$	$q_{Cap}$	$q_{Lab}$	$q_{Mat}$	$A{P}_{Cap}$	$A{P}_{Lab}$	$A{P}_{Mat}$	$q_{Out}$
Producteur 59	0.10	50.03K	105.40K	7.75K	1.91	0.91	12.30	95.39K
Producteur 73	0.88	40.60K	163.72K	13.60K	84.94	21.06	253.54	3.45M

• On remarque que le producteur 59 est le producteur le moins efficace techniquement avec une $TE=0.1$, c’est à dire qu’il n’est efficace dans l’allocation de ses inputs qu’à 10% (on peut d’ailleurs le constater en s’intéressant aux valeurs des productivités moyennes $A{P}_{Cap,Lab,Mat}$ qui sont très faibles).

• A l’inverse, le producteur 73 est le producteur le plus efficace techniquement avec une $TE=0.88$, c’est à dire qu’il est efficace dans l’allocation de ses inputs à 88%. Ce n’est pas étonnant étant donné les valeurs elevées des productivités moyennes.

• Enfin, les quantités d’inputs ne sont pas significativement plus importantes pour le producteur 73 et pourtant sa production est 36 fois plus elevée !

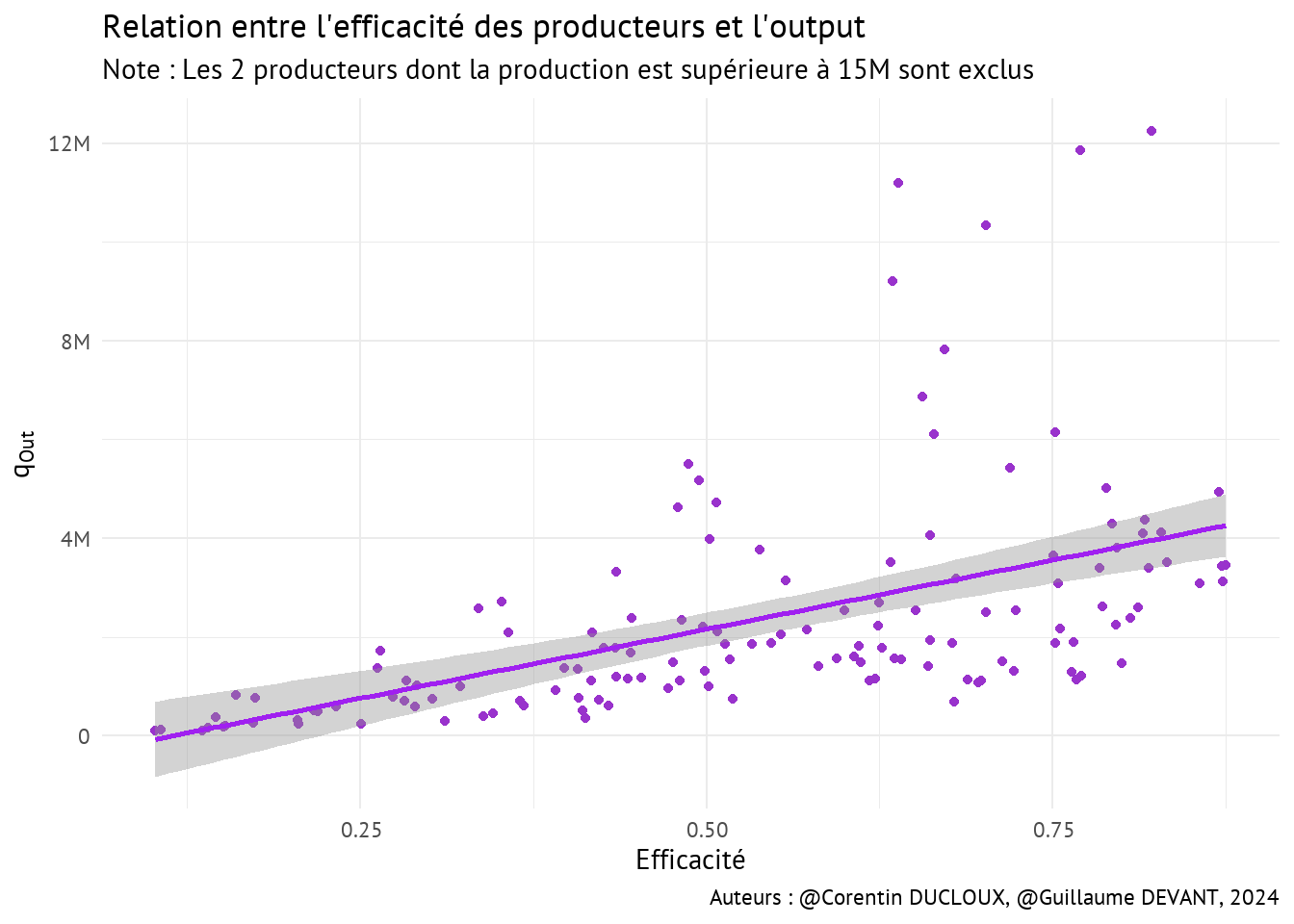
• Le graphique ci-dessus nous permet de constater qu’en moyenne, plus la production est elevée, plus l’efficacité du producteur estimée par le modèle Cobb-Douglas SFA le sera à son tour. Néanmoins, les producteurs dont la production est très importante ne sont pourtant pas les plus efficaces techniquement comme le montrent les quelques points qui se détachent de la tendance linéaire.

6.5.2 Tests statistiques

On va une fois de plus utiliser un test de rapport de vraisemblance.

Dans notre cas, on veut comparer le modèle Cobb-Douglas estimé par Moindres Carrés Ordinaires et le modèle Cobb-Douglas SFA estimé par la méthode du Maximum de Vraisemblance.

Les hypothèses du test sont les suivantes : $$\{\begin{array}{l}{H}_0:\text{Modele }1\Rightarrow \text{Ordinary Least Squares}\\ H_1:\text{Modele }2\Rightarrow \text{Error Component Frontier}\end{array}$$

La statistique de test est ${\lambda }_{LR}=2\cdot (\ln {\mathcal{L}}_1-\ln {\mathcal{L}}_2)$

• $\ln ({\mathcal{L}}_1)=$ -137.609

• $\ln ({\mathcal{L}}_2)=$ -133.889

$\Rightarrow$ Au risque $\alpha =5\mathrm{\%}$, la $p-value$ issue du test est égale à 0.003 $<0.05$, on rejette donc l’hypothèse nulle $H_0$, c’est à dire que le modèle de frontière de production Cobb-Douglas offre un meilleur ajustement.

Même si le modèle SFA a une log-vraisemblance légèrement inférieure au modèle Translog, il n’ajoute pas de problème de multicolinéarité et permet en plus d’estimer les scores d’efficacité des producteurs.

6.6 Fonction de production CES

Forme de la fonction

La fonction de production CES avec 3 variables explicatives s’écrit :

$$q_i=\gamma {\left(\sum _{i=1}^3{\delta }_k{x}_{ik}^{-\rho }\right)}^{-\frac{1}{\rho }}+{\epsilon }_i$$

Cependant, utiliser cette forme fonctionnelle peut s’avérer problématique car elle impose que toute paire d’inputs aient la même élasticité de substitution, soit par exemple que ${\sigma }_{\{\text{qCap, qLab}\}}={\sigma }_{\{\text{qCap, qMat}\}}$, alors même que c’est très loin d’être empiriquement vérifié. Une forme emboîtée permet de résoudre ce problème.

• La fonction de production CES emboîtée proposée par Sato (1967) dans notre cas s’écrit sous la forme :

$$q_{Out}=\gamma {[\delta \cdot {({\delta }_1{q}_{Cap}^{-{\rho }_1}+(1-{\delta }_1)q_{Lab}^{-{\rho }_1})}^{\frac{\rho }{{\rho }_1}}+(1-\delta )q_{Mat}^{-\rho }]}^{-\frac{1}{\rho }}+{\epsilon }_i$$

Nous estimerons cette fonction. ²

De part sa définition, la fonction CES est à rendements d’échelle constants.

ces_prod <- cesEst(
    "qOut",
    c("qCap", "qLab", "qMat"),
    data = apples,
    method = "SANN",
    returnGrad = TRUE,
)

Méthode d’optimisation SANN

Parmi les méthodes d’optimisation disponibles, aucune ne fonctionne à part celle du SANN (Simulated Annealing). La méthode SANN ou Recuit Simulé en français est une technique probabiliste pour approximer l’optimum global d’une fonction donnée.

Le nom provient du recuit en métallurgie. Pour plus de détail, voir la page wikipédia correspondante : https://en.wikipedia.org/wiki/Simulated_annealing

Fonction de production CES emboîtée
Variable dépendante : qOut
	Coefficients	Ecart Type	Pvalues	Significativité
$\gamma$	47.081	+/- 29.92	0.116
${\delta }_1$	−0.106	+/- 0.50	0.833
$\delta$	0.291	+/- 0.57	0.609
${\rho }_1$	−0.406	+/- 4.51	0.928
$\rho$	−0.448	+/- 1.31	0.733
Observations : 140                                              $R^2=$ 0.713
Elasticités de Substitution
Hicks-McFadden $\Rightarrow {\sigma }_{\text{{qCap, qLab}}}=$ 1.68
Allen-Uzawa $\Rightarrow {\sigma }_{\text{{qCap, qLab}}|\text{qMat}}=$ 1.81

Si le $R^2$ du modèle est plutôt bon, aucun coefficient n’est significatif.

• L’élasticité de substitution de Hicks-McFadden $\left(\frac{1}{1+{\rho }_1}\right)$ mesure la substituabilité entre les deux premiers facteurs de production, c’est à dire entre qCap et qLab. Les deux facteurs de production sont fortement substituables.

• L’élasticité de substitution de Allen-Uzawa $\left(\frac{1}{1+\rho }\right)$ est ici égale à 1.81. Celle-ci étant supérieure à 1, cela signifie que le facteur de production qMat est fortement substituable entre la combinaison des 2 autres facteurs de productions qCap et qLab. En d’autres termes, une augmentation du prix relatif d’une combinaison des 2 facteurs (qCap et qLab) entraînera une substitution vers qMat.

6.7 Machine Learning de production

Random Forest

À titre expérimental, il est envisageable d’explorer l’utilisation du Machine Learning pour étudier la production de pommes.

Cependant, compte tenu du peu de données disponibles, cette approche n’est pas idéale. Nous envisageons néanmoins d’appliquer un algorithme de Random Forest. Ce modèle permet d’extraire l’importance des variables, offrant ainsi une certaine transparence dans le fonctionnement de ce modèle de Machine Learning souvent perçu comme une boîte noire.

Comme pour les fonction de production nous tentons d’expliquer la variable qOut à partir des variables qLab, qCap et qMat.

• Effectuons un train-test split sur nos données.

apples_ML <- apples |> select(qOut, qCap, qLab, qMat)
split <- apples_ML |> initial_split(prop = 2 / 3)
df_train <- split |> training()
df_test <- split |> testing()

best_model <- ranger(
    formula = qOut ~ .,
    data = df_train,
    mtry = 1,
    min.node.size = 2,
    importance = "permutation"
)

Le coefficient de détermination $R^2$ associé à ce modèle de Random Forest est de 0.819, ce qui est similaire au score que nous avions obtenu précédemment.

Avec le graphique ci-dessous, nous pouvons comparer les valeurs prédites et les valeurs réelles. Lorsqu’un point est parfaitement aligné avec la ligne en pointillés rouge, le modèle fait la bonne prédiction. Cependant, si le point est au-dessus (resp. en-dessous) de la ligne, cela signifie que le modèle a sous-estimé (resp. surestimé) qOut.

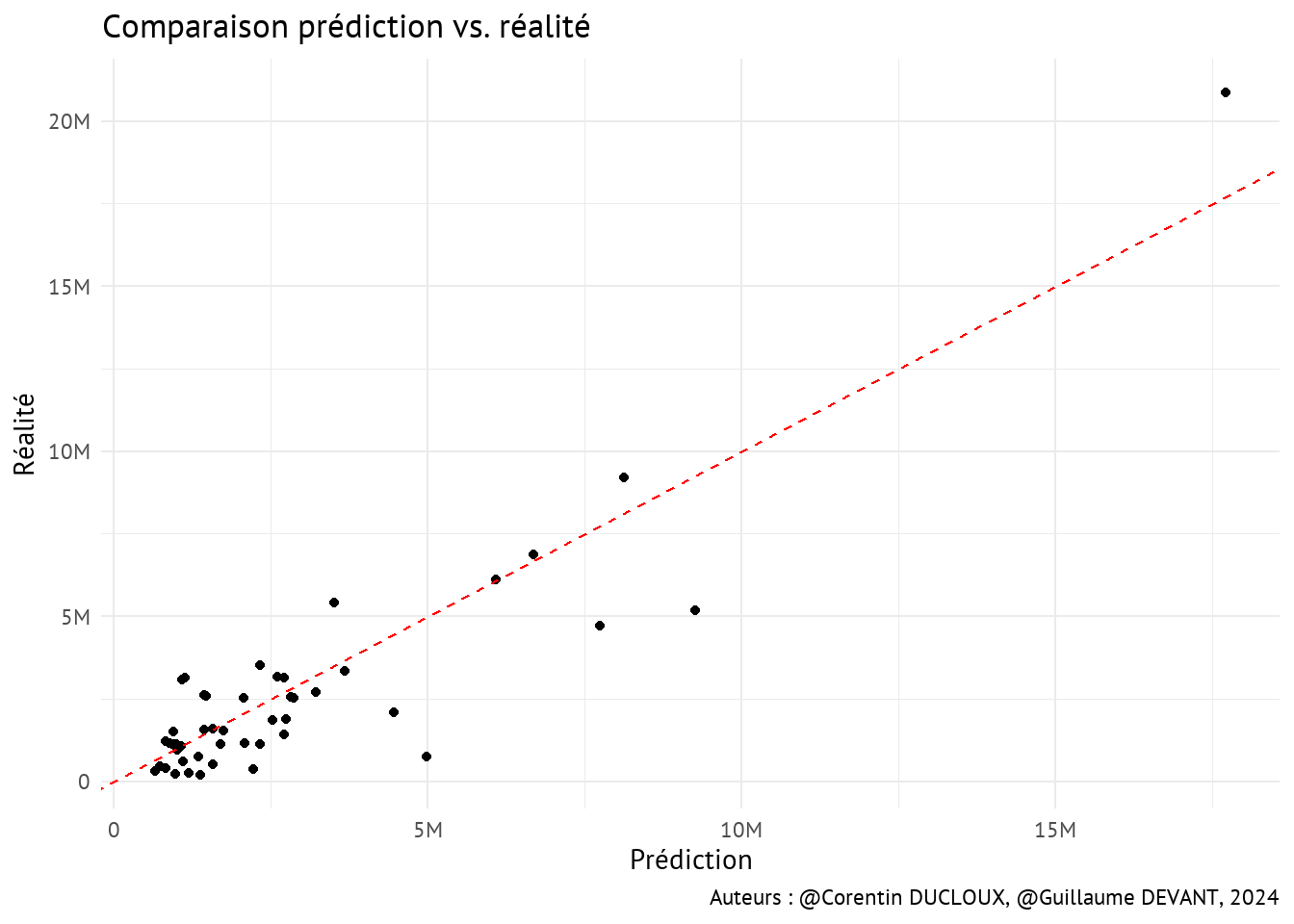
Lorsque l’on examine l’importance des variables, on observe que la variable qLab exerce le plus grand impact dans le modèle de Random Forest, tandis que la variable qCap a le moins d’influence. C’est en effet assez intéressant car la variable qLab est systématiquement significative dans les modèles précédents.

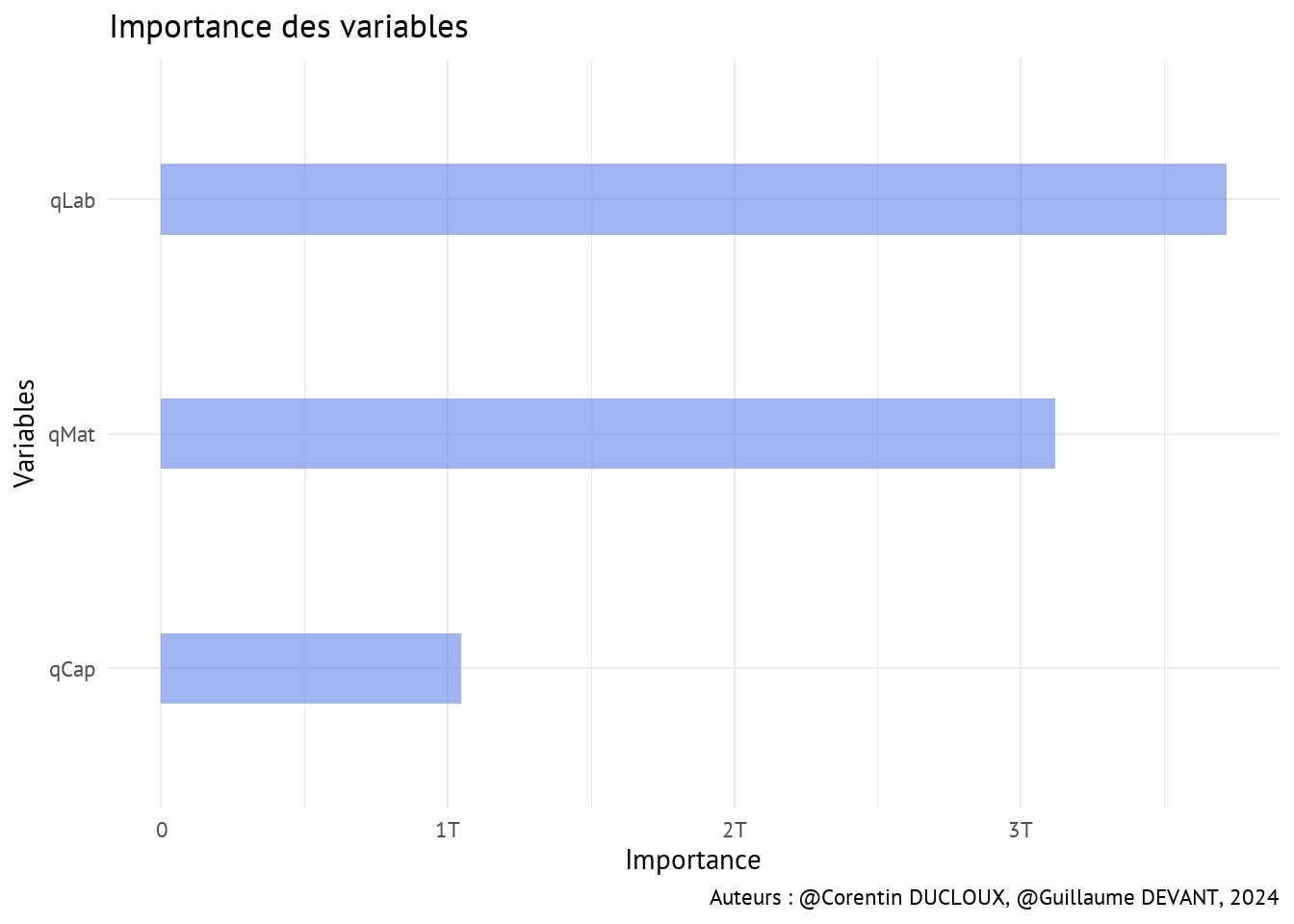
En résumé, dans notre contexte, le Machine Learning ne semble pas apporter une valeur ajoutée significative. Le modèle obtenu n’est pas plus performant que les modèles précédents, et nous perdons l’avantage de disposer de coefficients associés à chaque variable.

7 Fonctions de coût

D’un point de vue économétrique, l’utilisation d’une fonction de coût permet d’introduire un modèle beaucoup plus complet avec 4 équations : la fonction de coût et les 3 demandes d’inputs, et non pas une seule équation comme lorsqu’on utilise une fonction de production.

Une fonction de coût représente la relation entre les quantités des différents facteurs de production utilisés (ici qCap, qLab, qMat) et le coût total de production (ici vCap + vLab + vMat).

En fait, celle-ci donne le coût minimum associé à un niveau d’output et de prix des inputs, en tenant compte de la technologie disponible.

Calculons d’abord le coût total des inputs, c’est à dire $v_{Cap}+v_{Lab}+v_{Mat}$.

apples <- apples |> mutate(cost = vCap + vLab + vMat)

7.1 Fonction de coût Cobb-Douglas

Forme de la fonction

$$c_i=A\prod _{k=1}^3{p}_{ik}^{{\alpha }_k}{q}_i^{{\alpha }_y}{\epsilon }_i$$

• Dans notre cas la fonction de coût Cobb-Douglas s’écrit :

$$c_i=A\cdot q_{Out}^{{\alpha }_1}\cdot p_{Cap}^{{\alpha }_2}\cdot p_{Lab}^{{\alpha }_3}\cdot p_{Mat}^{{\alpha }_4}\cdot {\epsilon }_i$$

En linéarisant on obtient :

$$\ln (c_i)=\ln (A)+{\alpha }_1\cdot \ln (q_{out})+{\alpha }_2\cdot \ln (p_{Cap})+{\alpha }_3\cdot \ln (p_{Lab})+{\alpha }_4\cdot \ln (p_{Mat})+\ln ({\epsilon }_i)$$

cobb_cost <- translogCostEst(
    cName = "cost",
    yName = "qOut",
    pName = c("pCap", "pLab", "pMat"),
    apples, homPrice = FALSE,
    linear = TRUE
)

Fonction de coût Cobb-Douglas
Variable dépendante : ln(cost)
	Description	Coefficients	Ecart Type	Pvalues	Significativité
$A$	Constante du modèle	6.754	+/- 0.407	0	$\ast \ast \ast$
${\alpha }_1$	Coefficient associé à la variable ln(qOut)	0.373	+/- 0.031	0	$\ast \ast \ast$
${\alpha }_2$	Coefficient associé à la variable ln(pCap)	0.074	+/- 0.049	0.13
${\alpha }_3$	Coefficient associé à la variable ln(pLab)	0.465	+/- 0.147	0.002	$\ast \ast$
${\alpha }_4$	Coefficient associé à la variable ln(pMat)	0.486	+/- 0.081	0	$\ast \ast \ast$
Observations : 140
$R^2=$ 0.688
$R_{adj}^2=$ 0.679

• Le coefficient de 0.373 pour ln(qOut) signifie que si la production augmente de 1%, le coût total augmentera de 0.373%, ceteris paribus.

• Le coefficient de ln(pLab) est de 0.464. Cela indique qu’une augmentation d’1% du prix du travail entraîne une augmentation d’environ 0.464% du coût total, ceteris paribus.

• Le coefficient de ln(pMat) est de 0.486. Il indique qu’une augmentation d’1% du prix des matériaux entraine une augmentation d’environ 0.486% du coût total, ceteris paribus.

Seul le coefficient associé à la variable ln(pCap) n’est pas significatif, les autres le sont à 5 % et 10 % pour pLab.

7.1.1 Rendements d’échelle

Pour déterminer les rendements d’échelle dans le cas d’une fonction de coût Cobb-Douglas, il suffit d’utiliser la formule suivante : $\frac{1}{{\alpha }_1}$ avec ${\alpha }_1$ le coefficient associé à ln(qOut) $\Rightarrow$ c’est à dire l’inverse de l’élasticité de la production.

alpha_1 <- cobb_cost$coef[2] |> unname()

return_to_scale_cost <- 1 / alpha_1

• On trouve que $\frac{1}{{\alpha }_1}=$ 2.68 $\ne$ 1.47 trouvé dans la Section 6.2.1. Les rendements d’échelle sont donc toujours croissants, mais selon l’estimation de cette fonction de coût, ils le sont encore plus que dans le cas de la fonction de production.

7.2 Fonction de coût Cobb-Douglas de court terme

La fonction de court terme est définie par l’immutabilité d’au moins un facteur de production. Dans notre contexte, le capital est fixe, ce qui nous permet de la caractériser ainsi.

Forme de la fonction

$$c_i=A{x}_{i3}^{{\alpha }_f}\prod _{k=1}^2{p}_{ik}^{{\alpha }_k}{q}_i^{{\alpha }_y}{\epsilon }_i$$

• Dans notre cas la fonction de coût Cobb-Douglas de court terme s’écrit :

$$c_i=A\cdot q_{Out}^{{\alpha }_1}\cdot q_{Cap}^{{\alpha }_4}\cdot p_{Lab}^{{\alpha }_2}\cdot p_{Mat}^{{\alpha }_3}\cdot {\epsilon }_i$$

En linéarisant on obtient :

$$\ln (c_i)=\ln (A)+{\alpha }_1\cdot \ln (q_{out})+{\alpha }_4\cdot \ln (q_{Cap})+{\alpha }_2\cdot \ln (p_{Lab})+{\alpha }_3\cdot \ln (p_{Mat})+\ln ({ϵ}_i)$$

cobb_cost_ct <- translogCostEst(
    cName = "cost",
    yName = "qOut",
    pName = c("pLab", "pMat"),
    fNames = "qCap",
    data = apples,
    homPrice = FALSE,
    linear = TRUE
)

Fonction de coût Cobb-Douglas de court terme
Variable dépendante : ln(cost)
	Description	Coefficients	Ecart Type	Pvalues	Significativité
$A$	Constante du modèle	5.603	+/- 0.404	0	$\ast \ast \ast$
${\alpha }_1$	Coefficient associé à la variable ln(qOut)	0.279	+/- 0.032	0	$\ast \ast \ast$
${\alpha }_2$	Coefficient associé à la variable ln(pLab)	0.402	+/- 0.131	0.003	$\ast \ast$
${\alpha }_3$	Coefficient associé à la variable ln(pMat)	0.413	+/- 0.073	0	$\ast \ast \ast$
${\alpha }_4$	Coefficient associé à la variable ln(qCap)	0.237	+/- 0.038	0	$\ast \ast \ast$
Observations : 140
$R^2=$ 0.753
$R_{adj}^2=$ 0.746

• Le coefficient de 0.279 pour ln(qOut) signifie que si la production augmente de 1%, le coût augmentera de 0.279%, toutes choses étant égales par ailleurs.

• Le coefficient de la variable ln(qCap) est de 0.237, cela indique qu’une augmentation de 1% de la quantité de capital entraine une augmentation de 0.237% du coût total. A court terme, la quantité de capital a un impact positif et significatif sur le coût de production.

• Les prix du travail ln(pLab) et des matériaux ln(pMat) ont un impact moins important sur le coût total à court terme qu’à long terme, on le remarque car les coefficients sont moins élevés à court terme.

7.3 Comparaison Cobb-Douglas : Long Terme vs Court Terme

Comparasion des coefficients Cobb-Douglas
Variable dépendante : ln(cost)
Coefficients	LT	CT
Intercept	6.754	5.603
ln(qOut)	0.373	0.279
ln(pCap)	0.074	—
ln(pLab)	0.465	0.402
ln(pMat)	0.486	0.413
ln(qCap)	—	0.237

On remarque donc, à court terme, que la variation de la quantité produite (qOut) a moins d’impact sur le coût qu’à long terme. Dans les faits, à court terme, tous les coefficients sont plus bas. Ils sont contrebalancés par le coefficient de la quantité des capitaux (qCap) que le producteur possède.

7.4 Fonction de coût Translog

Forme de la fonction

$$\begin{array}{c}\ln (c_i)=\alpha +\sum _{k=1}^3{\beta }_k\ln (p_{ik})+{\alpha }_q\ln (q_i)\\ +\frac{1}{2}\sum _{l=1}^3\sum _{k=1}^3{\beta }_{kl}\ln (p_{ik})\ln (p_{il})\frac{1}{2}{\alpha }_q(\ln (q_i){)}^2\\ +\frac{1}{2}\sum _{k=1}^3{\alpha }_{kq}\ln (p_{ik})\ln (q_i)+{\epsilon }_i\end{array}$$

• Dans notre cas la fonction de coût Translog s’écrit :

$$\begin{array}{c}\ln (c_i)=\alpha +{\beta }_2\ln (p_{Cap})+{\beta }_3\ln (p_{Lab})+{\beta }_4\ln (p_{Mat})+{\beta }_1\ln (q_{Out})+[\frac{1}{4}{\beta }_{11}(\ln (q_{Out}){)}^2]\\ [({\beta }_{22}\ln (p_{Cap}^2)+{\beta }_{33}\ln (p_{Lab}^2)+{\beta }_{44}\ln (p_{Mat}^2)+{\beta }_{23}\ln (p_{Cap}{p}_{Lab})+{\beta }_{24}\ln (p_{Cap}{p}_{Mat})+{\beta }_{34}\ln (p_{Lab}{p}_{Mat})]+\\ \frac{1}{2}[{\beta }_{12}\ln (p_{Cap})\ln (q_{Out})+{\beta }_{13}\ln (p_{Lab})\ln (q_{Out})+{\beta }_{14}\ln (p_{Mat})\ln (q_{Out})]+{\epsilon }_i\end{array}$$

translog_cost <- translogCostEst(
    cName = "cost",
    yName = "qOut",
    pName = c("pCap", "pLab", "pMat"),
    data = apples,
    homPrice = FALSE
)

Fonction de coût Translog
Variable dépendante : ln(cost)
	Description	Coefficients	Ecart Type	Pvalues	Significativité
$\alpha$	Intercept	25.383	+/- 3.511	0	$\ast \ast \ast$
${\beta }_1$	ln(qOut)	−2.04	+/- 0.511	0	$\ast \ast \ast$
${\beta }_2$	ln(pCap)	0.199	+/- 0.538	0.712
${\beta }_3$	ln(pLab)	−0.025	+/- 2.232	0.991
${\beta }_4$	ln(pMat)	−1.245	+/- 1.201	0.302
${\beta }_{11}$	ln(qOut²)	0.164	+/- 0.041	0	$\ast \ast \ast$
${\beta }_{12}$	ln(qOut)*ln(pCap)	−0.028	+/- 0.043	0.513
${\beta }_{13}$	ln(qOut)*ln(pLab)	0.008	+/- 0.171	0.965
${\beta }_{14}$	ln(qOut*ln(pMat)	0.049	+/- 0.092	0.598
${\beta }_{22}$	ln(pCap²)	−0.095	+/- 0.105	0.367
${\beta }_{23}$	ln(pCap)*ln(pLab)	−0.746	+/- 0.244	0.003	$\ast \ast$
${\beta }_{24}$	ln(pCap)*ln(pMat)	0.182	+/- 0.13	0.165
${\beta }_{33}$	ln(pLab²)	−0.503	+/- 0.943	0.595
${\beta }_{34}$	ln(pLab)*ln(pMat)	0.139	+/- 0.433	0.748
${\beta }_{44}$	ln(pMat²)	0.529	+/- 0.338	0.12
Observations : 140
$R^2=$ 0.768
$R_{adj}^2=$ 0.742

• On remarque qu’avec une fonction de coût Translog, le coût dépend majoritairement de la quantité produite, on le constate avec la significativité des coefficients associés à ln(qOut) et ln(qOut²).

Le problème dans notre cas avec la fonction de coût translog est que nous n’avons que quatre coefficients significatifs sur les 15 estimés. Cela rend la fonction plus difficile à estimer pour effectuer des prédictions, et les résultats ne sont pas nécessairement plus intéressants ni meilleurs que ceux de la fonction Cobb-Douglas de court terme que nous avions estimée précédemment (on peut notamment s’en convaincre en comparant les valeurs de $R_{adj}^2$ des deux modèles).

8 Profit des producteurs

8.1 Analyse du profit

$$\pi =(p_{Out}\cdot q_{Out})-\stackrel{cost}{\overbrace{(v_{Cap}+v_{Lab}+v_{Mat})}}$$

apples <- apples |> mutate(profit = (pOut * qOut) - cost)

Note

• Les producteurs dont le profit dépasse 5 millions sont mis en surbrillance verte.
• Les producteurs dont le profit est négatif sont en mis subrillance rouge.

Profit des producteurs de pommes

\(N\)

\(\pi\)

Producteur 129

64.15M

Producteur 96

38.05M

Producteur 132

28.85M

Producteur 134

18.69M

Producteur 66

12.52M

Producteur 41

12.19M

Producteur 137

11.27M

Producteur 90

9.67M

Producteur 16

7.92M

Producteur 103

7.76M

1–10 of 140 rows

...

On remarque tout de même qu’il y a d’importantes différences de profits entre les producteurs.

En effet, il y a 14 producteurs de pommes ayant un profit négatif et 20 producteurs dont le profit est supérieur à 5 millions.

• Le profit moyen $\overline{\pi }$ quant à lui est de 2957490.

• Le profit médian $\tilde{\pi }$, bien inférieur, est de 862843.6.

Enfin, le producteur 53 possède le profit le moins elevé du panel et le producteur 129 possède le profit le plus elevé (voir le tableau ci-dessus).

On remarque quelque chose d’intéressant : la médiane des profits des producteurs recevant des conseils est bien plus élevée (1049160) que ceux ne recevant pas de conseils (709112.3)

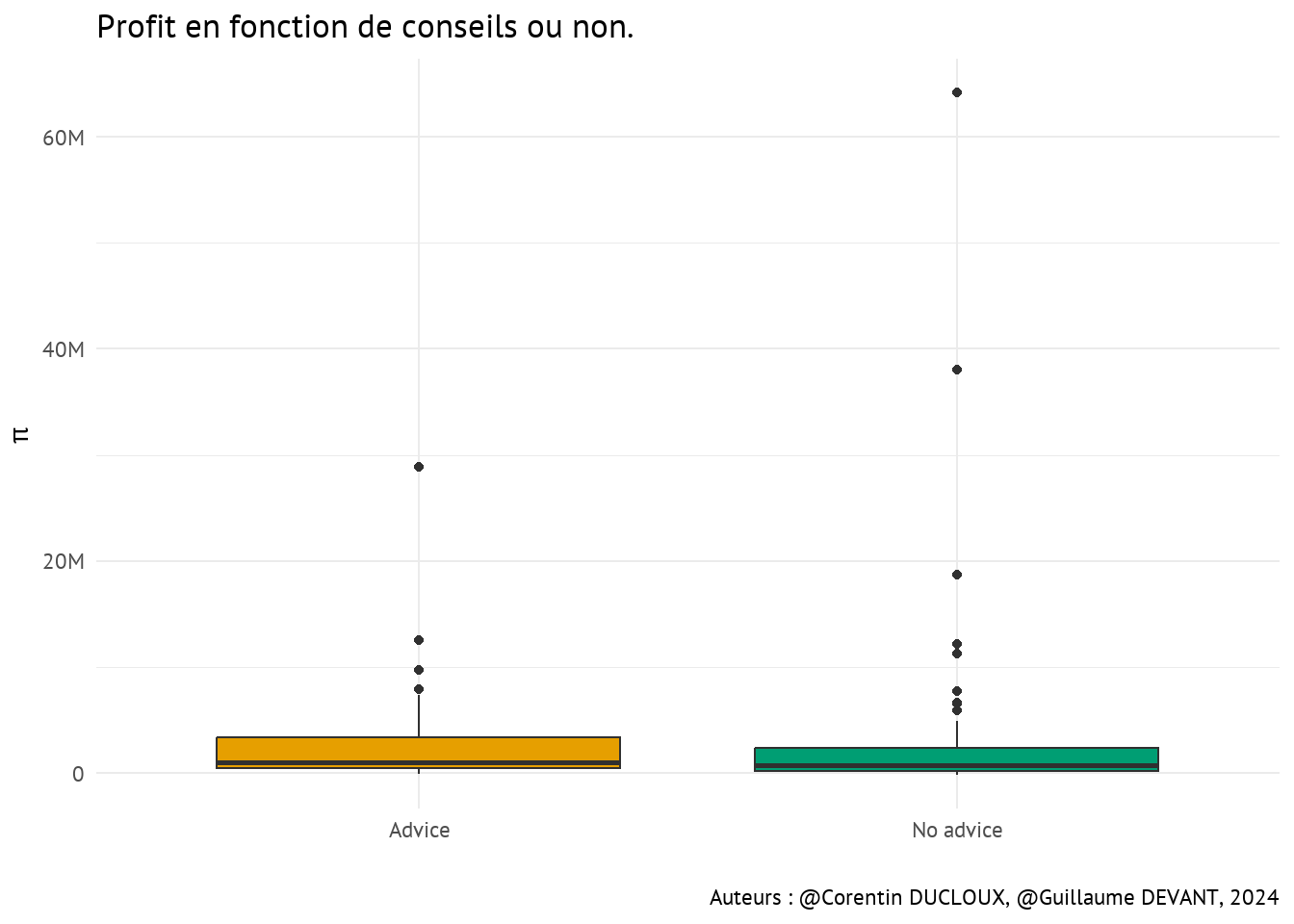
Nous pouvons aussi nous intéresser au nuage de points des profits et des quantités produites.

Note : Etant donné la corrélation de 0.91 entre profit et qOut, on s’attend évidemment à ce que produire plus de pommes entraîne nécessairement un acroissement du profit.

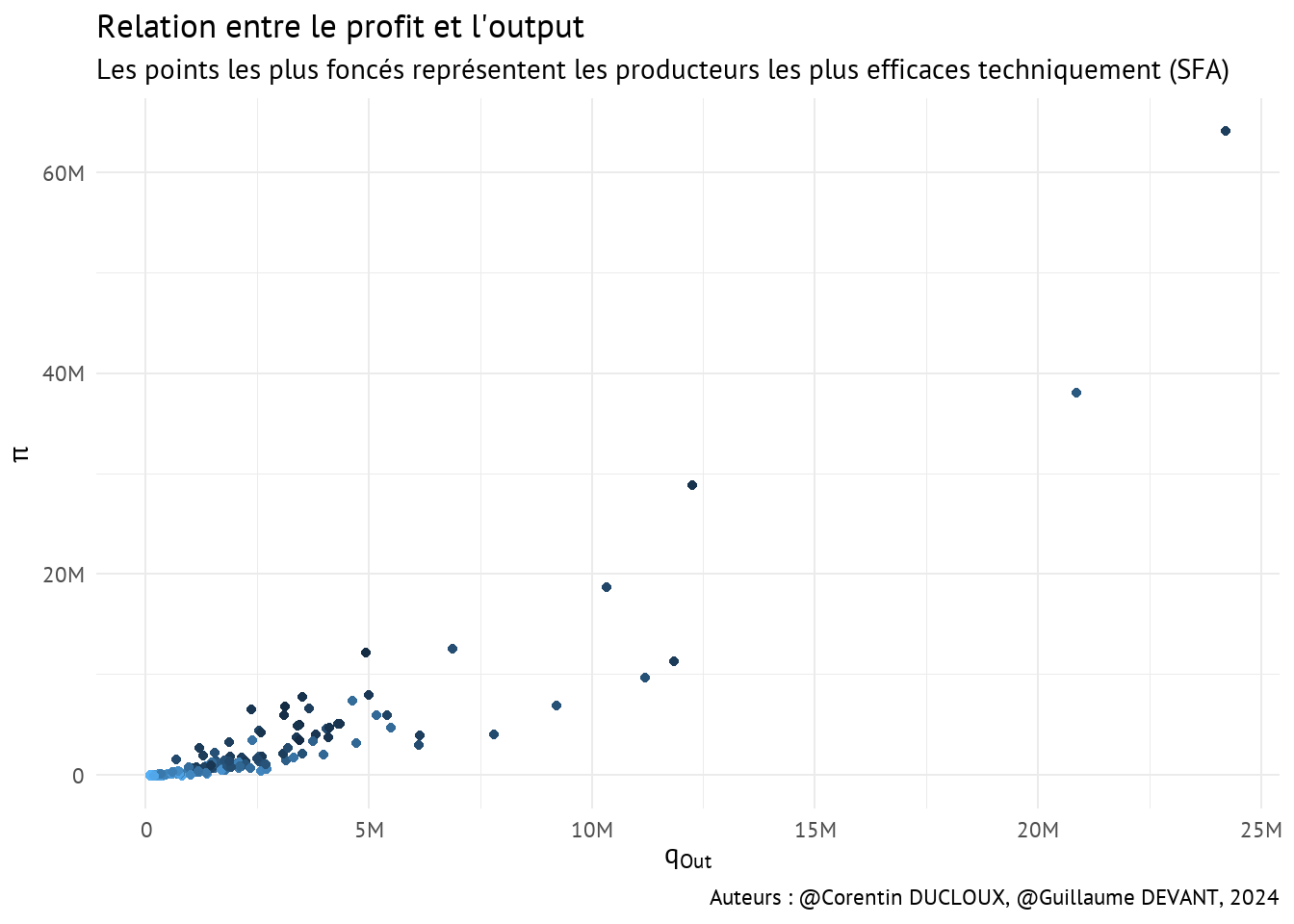
On peut également tracer les courbes correspondant à la recette totale (RT) et au coût total (CT). La relation entre RT et la quantité produite est estimée de manière quadratique alors que la relation entre le CT et la quantité produite est une relation linéaire. Les points correspondent aux données réelles.

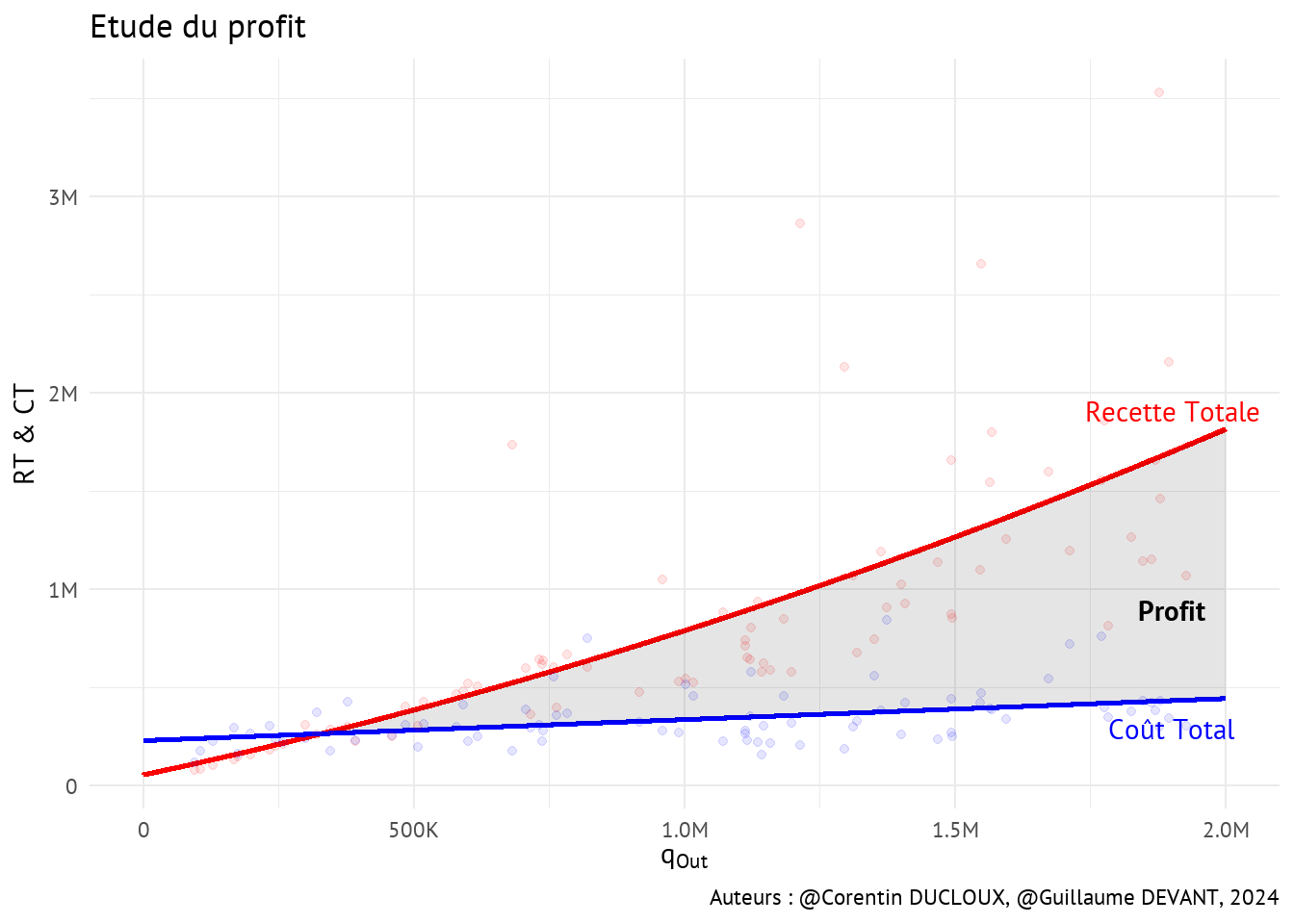
On constate que le profit est dans un premier temps négatif puis devient positif (partie grisée). Ce petit modèle permet de constater à partir de quelle quantité produite un arboriculteur commence à faire du profit.

On remarque aussi visuellement les rendements d’échelle croissants

8.2 Fonction de profit Quadratique Normalisée Symétrique

La fonction a été introduite par Kohli (1993). Cette forme flexible permet d’estimer les profits et d’imposer globalement des conditions sur la courbure requise (si nécessaire d’imposer la convexité des prix).

Forme de la fonction

$$\pi (p)=\sum _{i=1}^4{\alpha }_i{p}_i+\frac{1}{2}{\left(\sum _{i=1}^4{\theta }_i{p}_i\right)}^{-1}\sum _{i=1}^4\sum _{j=1}^4{\beta }_{ij}{p}_i{p}_j$$

Avec $\pi$ le profit, $p_i$ le prix des netputs, ${\theta }_i$ le poids des prix pour la normalisation et ${\alpha }_i$, ${\beta }_{ij}$ les coefficients à estimer.

Note : la notation netput correspond au cas où l’output est traité comme une quantité positive et les inputs sont traités comme négatifs.

• Transformons donc les inputs qCap, qLab et qMat préalablement.

apples_snq <- apples |>
    select(N, pOut, pCap, pLab, pMat, qOut, qCap, qLab, qMat) |>
    mutate(qCap = -qCap, qLab = -qLab, qMat = -qMat)

• Nous pouvons maintenant estimer la fonction. A noter cependant que la première estimation de la fonction de profit n’est pas convexe dans les prix des netputs ! La commande snqProfitImposeConvexity permet de régler ce problème.

snq_func <- snqProfitEst(
    priceNames = c("pOut", "pCap", "pLab", "pMat"),
    quantNames = c("qOut", "qCap", "qLab", "qMat"),
    form = 0,
    data = apples_snq
)

snq_func_convex <- snqProfitImposeConvexity(snq_func, stErMethod = "coefSim", nRep = 50)

Fonction de profit SNQ
Variable dépendante : profit
	Coefficients	Ecart Type	Significativité
${\alpha }_1$	1.75M	+/- 222.95K	$\ast \ast \ast$
${\alpha }_2$	−160.92K	+/- 41.90K	$\ast \ast \ast$
${\alpha }_3$	−224.31K	+/- 27.99K	$\ast \ast \ast$
${\alpha }_4$	−289.38K	+/- 22.14K	$\ast \ast \ast$
${\beta }_{11}$	117.46K	+/- 114.95K
${\beta }_{12}$	−41.90K	+/- 48.87K
${\beta }_{13}$	−116.57K	+/- 40.42K	$\ast \ast$
${\beta }_{14}$	41.00K	+/- 38.00K
${\beta }_{21}$	−41.90K	+/- 48.87K
${\beta }_{22}$	200.69K	+/- 37.25K	$\ast \ast \ast$
${\beta }_{23}$	−63.91K	+/- 23.13K	$\ast \ast$
${\beta }_{24}$	−94.88K	+/- 24.57K	$\ast \ast \ast$
${\beta }_{31}$	−116.57K	+/- 40.42K	$\ast \ast$
${\beta }_{32}$	−63.91K	+/- 23.13K	$\ast \ast$
${\beta }_{33}$	175.58K	+/- 21.94K	$\ast \ast \ast$
${\beta }_{34}$	4.89K	+/- 26.90K
${\beta }_{41}$	41.00K	+/- 38.00K
${\beta }_{42}$	−94.88K	+/- 24.57K	$\ast \ast \ast$
${\beta }_{43}$	4.89K	+/- 26.90K
${\beta }_{44}$	48.99K	+/- 26.84K	$\ast$
$R^2$ — profit $=$ 0.189
$R^2$ — qOut $=$ 0.015
$R^2$ — qCap $=$ 0.173
$R^2$ — qLab $=$ 0.073
$R^2$ — qMat $=$ -0.052

8.2.1 Elasticités-prix

Définition

Une élasticité-prix est définie par :

$$E_{ij}={\displaystyle \frac{{\displaystyle \frac{\partial q_i}{q_i}}}{{\displaystyle \frac{\partial p_j}{p_j}}}}={\displaystyle \frac{\partial q_i}{\partial p_j}}\cdot {\displaystyle \frac{p_j}{q_i}}$$

On peut facilement obtenir les estimations des élasticités-prix aux prix moyens et aux quantités moyennes.

Elasticités-prix des netputs
	$p_{Out}$	$p_{Cap}$	$p_{Lab}$	$p_{Mat}$
$q_{Out}$	0.049	0.003	−0.055	0.003
$q_{Cap}$	−0.068	−0.327	0.187	0.208
$q_{Lab}$	0.621	0.100	−0.716	−0.006
$q_{Mat}$	−0.037	0.139	−0.007	−0.095

• Par exemple, $E_{\left\{q_{Cap};p_{Cap}\right\}}=-0.327$, c’est à dire que quand le prix du capital augmente de 1%, la quantité de capital va diminuer de 0.327%.

• D’autre part, pour $E_{\left\{q_{Lab};p_{Cap}\right\}}=0.1$, on voit que quand le prix du capital augmente de 1%, la quantité de travail va augmenter de 0.1%.

Conclusion : On voit bien à travers ce tableau l’ensemble des substitutions qui peuvent s’effectuer

8.3 Analyse du coût moyen

Le coût moyen représente le coût total (cost) de la firme divisé par son niveau d’output (qOut).

apples <- apples |> mutate(CM = cost / qOut)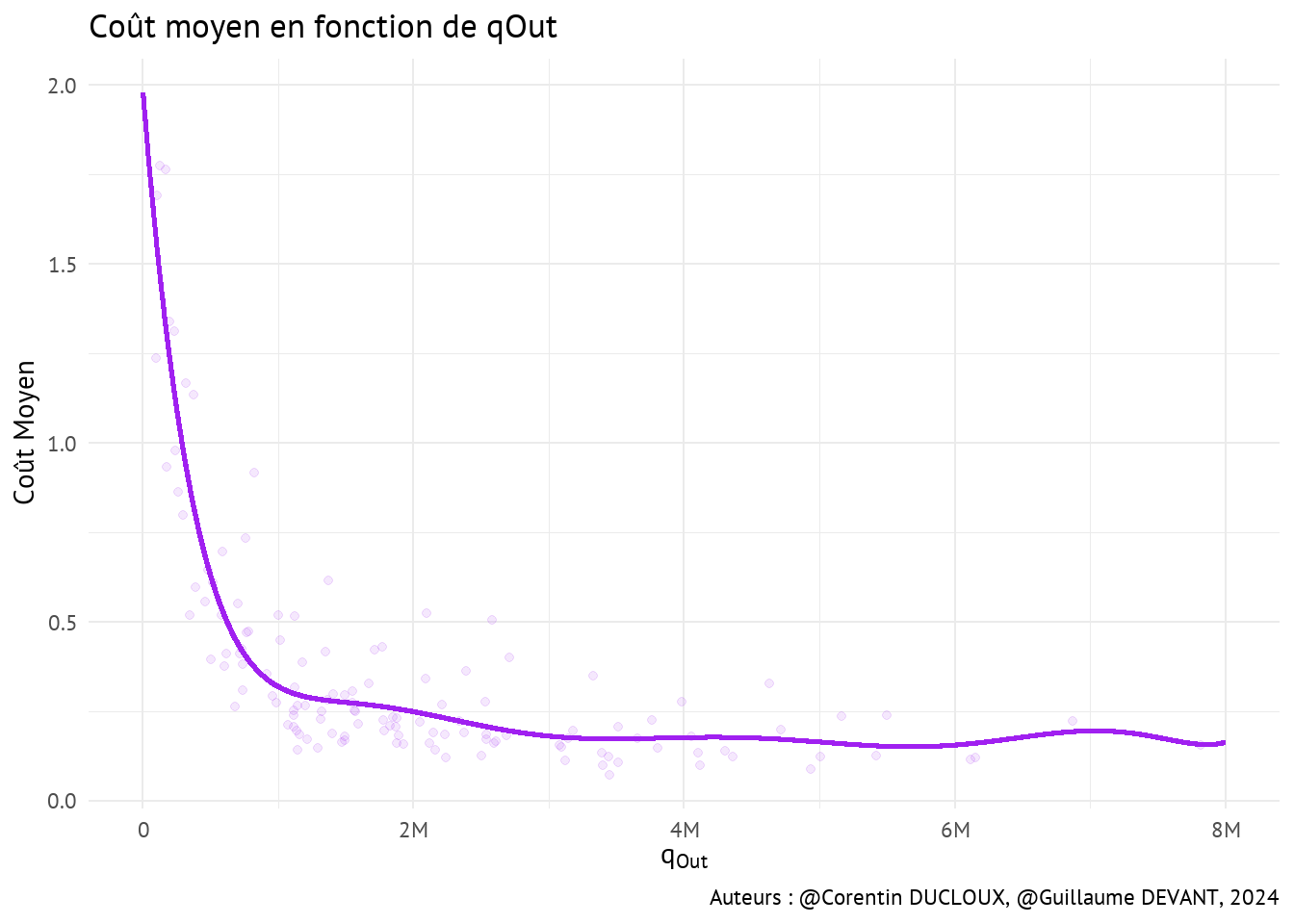

• On constate que le coût moyen diminue considérablement au début de la production, puis se stabilise à mesure que la quantité produite augmente.

---

On peut ensuite analyser la différence entre le coût marginal et le coût moyen (le coût marginal que nous utilisons est celui calculé en Section 5.4.1).

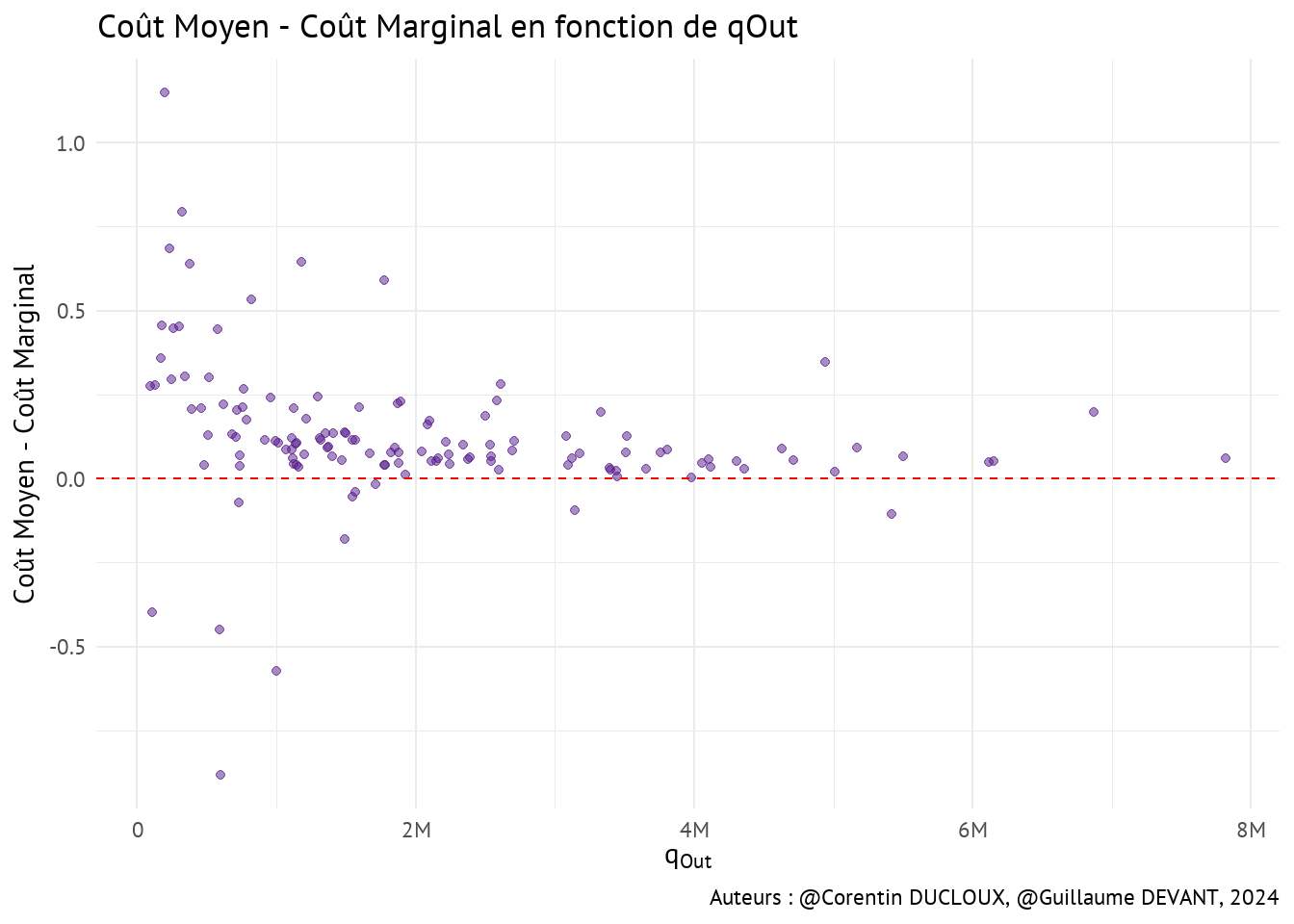
Selon Harnay (2024), toutes les valeurs négatives démontrent donc que les producteurs ont un coût marginal croissant, tandis que si la valeur est positive sur ce graphe, cela signifie que le producteur a un coût marginal décroissant. On constate que la majorité des producteurs ont un coût marginal décroissant.

9 Conclusion

L’utilisation de l’économétrie pour étudier la production, les coûts et le profit permet d’apporter un cadre particulièrement pertinent pour analyser les facteurs utilisés dans la production des pommes. On a notamment constaté que, bien qu’élémentaire, la fonction Cobb-Douglas fournit généralement beaucoup plus d’informations qu’une fonction linéaire ou quadratique, en étant moins complexe qu’une fonction Translog, généralement plus difficile à interpréter et à utiliser en raison du grand nombre de coefficients impliqués, pour des résultats pas toujours très pertinents. De plus, dans les cas où l’on rencontre de l’inefficacité, on peut obtenir de meilleurs résultats avec un modèle SFA, que nous avons notamment utilisé pour estimer la production. Dans les faits, quelles que soient les variables étudiées, on ne peut pas affirmer qu’une fonction est meilleure qu’une autre. Certaines permettent d’estimer les coûts marginaux (Translog), d’autres les productivités marginales (Cobb-Douglas, Quadratique, Translog), les élasticités de substitutions (CES) ou encore les élasticités-prix (SNQP). C’est pourquoi nous pensons que dans le cas où l’on souhaite étudier les coûts, la production ou encore le profit, il est nécessaire d’examiner tous ces outils et de croiser les résultats pour avoir une idée générale du sujet que l’on traite.

Haut de la page

Les références

Harnay. 2024. « Coûts marginaux ». Dictionnaire de droit de la concurrence, nᵒ Art. N° 12207.

Henningsen, Arne. 2017. « Package micEcon ».

Ivaldi, Marc, Norbert Ladoux, Hervé Ossard, et Michel Simioni. 1996. « Comparing Fourier and translog specifications of multiproduct technology: Evidence from an incomplete panel of French farmers ». Journal of applied econometrics 11 (6): 649‑67.

Kohli, Ulrich. 1993. « A symmetric normalized quadratic GNP function and the US demand for imports and supply of exports ». International Economic Review, 243‑55.

Sato, Kazuo. 1967. « A two-level constant-elasticity-of-substitution production function ». The Review of Economic Studies 34 (2): 201‑18.

Wickham, Hadley. 2014. « Tidy Data ». Journal of Statistical Software.

Notes de bas de page

1. Grâce à cet argument, on restreint en fait les coefficients de tous les termes quadratiques et d’interaction à zéro, ce qui revient à estimer une fonction Cobb-Douglas.

2. L’estimation d’une fonction CES emboîtée à 3 inputs est disponible dans le package micEconCES.